Linear Algebra Raw

Week 0

1. A reference to all symbols necessary for the notes Linear Algebra Symbols
2. A list of Problems associated with the Notes 471-ProblemList
3. A series of unanswered questions about Linear Algebra 471-QuestionBank
4. References to Category theory Category Theory For Babies Category Theory
5. Tikz Testing Ground 471-ImagesTest 6) 471-Homework

Coordinate Maps $[\cdot {]}_B$

Given a Vector Space V over F, and a basis $B=\{v_1,..,v_n\}\subseteq V$, a coordinate map is the following isomorphism:

$$\begin{array}{rl}[\cdot {]}_B:V& \to F^{dimV=n}\\ v\mapsto [v{]}_B=(a_1,...,a_n)& \end{array}$$

Where $u={\sum }_{i=1}^n{a}_i{u}_i$

Week 1

Lecture 1 : Systems of Equations

Solution Space

Given a field F, and a system of m equations and n variables,

$$\begin{array}{rl}{a}_{11}{x}_1+a_{12}{x}_2+...a_{1n}{x}_n& =y_1\\ & ⋮\\ a_{m1}{x}_1+a_{m2}{x}_2+...+a_{mn}{x}_n& =y_m\end{array}$$

A solution space is the set of all n-tuple $(b_1,...,b_n)\in F^n$ such that it solves all of the equations. Can be either of the three cases

1. The system is not solvable Then there are no solutions to the system,
2. The system is solvable Then there are either 1 or infinitely many solutions (cannot have any other finite number of solutions other than 1, think about lines intersecting)

Back Substitution

A method of solving a system of equations where the equations are shaped like a triangle, with no 0’s on the diagonals!

Example

$$\begin{array}{rl}{a}_{11}{x}_1+a_{12}{x}_2+...+a_{1(n-1)}{x}_{n-1}+a_{1n}{x}_n& =y_1\\ a_{22}{x}_2+...a_{2(n-1)}{x}_{n-1}+a_{2n}{x}_n& =y_2\\ & ⋮\\ a_{(m-1)(n-1)}{x}_{n-1}+a_{(m-1)n}{x}_n& =y_{m-1}\\ a_{mn}{x}_n& =y_m\\ \Updownarrow & \end{array}$$ $$\begin{array}{rl}{x}_1& =\frac{1}{a_{11}}(y_1-...)\\ & ⋮\\ x_{n-1}& =\frac{1}{a_{(n-1)(n-1)}}(y_{m-1}-\frac{y_m}{a_{mn}})\\ x_n& =\frac{1}{a_{mn}}{y}_m\end{array}$$

$a_{ii}\ne 0,i\in [n]$, OR WE GET DIVISION BY ZERO!

We assume that

Unique Solution

$$\begin{array}{rl}1x_1+x_2& =-2\\ 3x_2& =1\end{array}\Rightarrow x_2=\frac{1}{3}\Rightarrow 2x_1+\frac{1}{3}=-2\Rightarrow x_1=\frac{-2-1/3}{2}$$

Unique solution

$$\begin{array}{rl}{x}_1& =-7/6\\ x_2& =1/3\end{array}$$

Infinitely Many Solutions

$$\begin{array}{rl}0x_1+2x_2& =-2\\ 3x_2& =6\end{array}$$

Note, this system has Infinitely many solutions! $x_2=2\Rightarrow =0x_1=2\cdot 2=4\Rightarrow 0=0$ Hence, we can form a solution space $(c,2)$, where $c\in F$

Symbolic representation of systems of linear equations

We can represent any system in the following way : $A=(a_{ij})i\in [m],j\in [n],a_{ij}\in F$ $Ax=y,x=(x_1,...,x_n),y\in F^n$

Lecture 2 : E.R.O and Equivalent Systems

Elementary Row Operations (ERO)

Operations that can be done on any system with the following properties

1. Scalar Multiplication : $M_i(a)$ : multiply the ith equation by a, where $a\ne 0$
2. Addition : $A_{i\to j}:(a)$ replace the jth equation with jth equation + a $\times$ ith equation, $a\ne 0$
3. Permutation : $P_{ij}$ : Swap ith and jth equation

Row equivalent

We call 2 systems row equivalent if one is obtained from another by a sequence of elementary row operations

Theorem 1.1 Equivalent Systems of Equations

Two systems, $Ax=y$ and $A^{\prime }x=y^{\prime }$ are equivalent $⟺$ they have the same solution space

Theorem 1.2 : Row Equivalence $\Rightarrow$ Equivalent Systems

Proof $Ax=y$ and $A^{\prime }x=y^{\prime }$ that are tow equivalent, then

$$Ax=y\to (i_1)\to ...\to (i_k)\to A^{\prime }x=y^{\prime }$$

3. $A_{ij}$ produces equivalent systems Suppose we have two systems, $Ax=y$ and $A^{\prime }x=y^{\prime }$ that have the same solution with the following condition : $a_{i1}^{\prime }{x}_1+...+a_{in}^{\prime }{x}_n=y_i$ $a_{j1}^{\prime }{x}_1+...+a_{jn}^{\prime }{x}_n=y_j$ Apply the $A_{ij}$ operation on the system, then

You must prove it for each individual operation

Corollary 1.3 : Homogenous row Equivalent Systems $Ax=0$ and $A^{\prime }x=0$ be two two row equivalent matrices, then they exactly have the same solution!

Example

$$\begin{array}{ccccccccc}2x_1& -& x_2& +& 2x_3& +& 2x_4& =& 0\\ x_1& +& 4x_2& & & -& x_4& =& 0\\ 2x_1& +& 6x_2& -& x_3& +& 5x_4& =& 0\end{array}$$

Theorem 1.2 Solutions to Equivalent homogenous systems

Row-Reduced Echelon Form (RREF)

A system of linear equations is in RREF if it follows the follow requirements

1. The first non-zero entry in each row is equal to 1
2. Each column of the system contaisn the leading non-zro entry for some row has all its other entries 0

Lecture 3 :

• Added Example to RREF example

Week 2

Lecture 4 :

affine space

Ring

Field

Week 8

Lecture 20

Theorem :

$e_1,E_1,{\mathcal{E}}_1,{\mathbb{E}}_1$

Theorem

Given a basis $B=\{v_1,...,v_n\}\subseteq V$,a linear map

$$T:V\to W$$

is the same thing as an n-tuple of vectors $w_1,...,w_n\in W$ Namely

• Given $T$, define an n-tuple as : $w_1=T(v_1),...,w_n=T(v_n)$
• Conversely, given $w_1,...,w_n$, define $T$ by declaring that $T(v_1)=w_1,..,T(v_n)=w_n$
• This allows us to uniquely define a linear transformation $T:V\to W$ such that

$$T\left(\sum _i{a}_i{v}_i\right)=\sum _i{a}_{i}T(v_i)$$

To be even more explicit, we can define W with a basis of $C=\{w_1^{\prime },...,w_n^{\prime }\}$

Examples

1. Polynomials of fixed degrees : Describing their Transformations Lets choose a standard basis for $F[x{]}_{\le 2}$ to be $B=\{1,x,x^2\}$. Then we could choose a triple $(p_1(x),p_2(x),p_3(x)),p_i(x)\in F[x{]}_n$. Using Threom 0.0.0., the transformation $T$ is defined by the following $\begin{array}{rl}1& \to p_1(x)\\ x& \to p_2(x)\\ x^2& \to p_3(x)\\ \text{ In General}& \\ T(a+bx+c{x}^2)& =a{p}_1(x)+b{p}_2(x)+c{p}_3(x)\end{array}$

Definition : $[T{]}_C^B$

To denote the matrix of $T$ relative to the ordered Bases $B\subseteq V,C\subseteq W$ is

$$[T{]}_C^B=\left[\begin{array}{cccccc}[T(v_1){]}_C& [T(v_2){]}_C& \dots & [T(v_j){]}_C& \dots & [T(v_m){]}_C\end{array}\right]$$

Where number of rows $=dimW$ and number of columns is $dimV$

Note

$$[T{]}_C^B=(a_{ij}),1\le i\le dimW1\le j\le dimV$$

Or each basis vector as : $T{v}_j={\sum }_{i=1}^m{a}_{ij}{w}_i⟺[T{v}_j{]}_C=\left[\begin{array}{c}{a}_{1j}\\ ⋮\\ a_m\end{array}\right]$

Exercises

Rotations on ${\mathbb{R}}^2$ Lets denote the rotations on ${\mathbb{R}}^2$ as the following transformation

$$R_{\alpha }:{\mathbb{R}}^2\to {\mathbb{R}}^2$$

and the Standard Basis $SB=\{e_1,e_2\}\subseteq {\mathbb{R}}^2$, then

$$[R_{\alpha }(e_1){]}_{SB}=\left[\begin{array}{c}\cos (\alpha )\\ \sin (\alpha )\end{array}\right]$$

$$[R_{\alpha }(e_2){]}_{SB}=\left[\begin{array}{c}\cos (\pi +\alpha )\\ \sin (\pi +\alpha )\end{array}\right]=\left[\begin{array}{c}-\sin (\alpha )\\ \cos (\alpha )\end{array}\right]$$

Therefore, the Matrix for rotations on the cartesian plane is :

$$[R_{\alpha }{]}_{SB}^{SB}=\left[\begin{array}{cc}\cos (\alpha )& -\sin (\alpha )\\ \sin (\alpha )& \cos (\alpha )\end{array}\right]$$

We used the following properties(which we will prove later!) : $\begin{array}{rl}\cos (x+\frac{\pi }{2})& =\cos (x)\cos (\frac{\pi }{2})-\sin (x)\sin (\frac{\pi }{2})=-\sin (x)\\ \sin (x+\frac{\pi }{2})& =\sin (x)\cos (\frac{\pi }{2})+\cos (x)\sin (\frac{\pi }{2})=\cos (x)\end{array}$

$F:{\mathbb{R}}^3\to {\mathbb{R}}^3,F(x_1,x_2,x_3)=(x_1+2x_2,2x_1-x_2+3x_3)$ Lets denote the standard basis $SB=\{e_1,e_2,e_3\}\subseteq {\mathbb{R}}^3,\{e_1,e_2\}\subseteq {\mathbb{R}}^2$ to each vector space respectively. Then

$$\begin{array}{rl}T(e_1)& =T(1,0,0)=(1+0,2-0+0)=(1,2)\\ T(e_2)& =T(0,1,0)=(0+2,0-1+0)=(2,-1)\\ T(e_3)& =T(0,0,1)=(0+0,0-0+3)=(0,3)\end{array}$$ $$[F{]}_{SB}^{SB}\left[\begin{array}{ccc}1& 2& 0\\ 2& -1& 3\end{array}\right]$$

Write the matrix $[T{]}_{SB}^{SB}$ for the following transformation

$$\begin{array}{rl}T:F[x{]}_{\le 2}& \to F[x{]}_{\le 4}\\ 1& \to p_1(x)=1+x=1+1\cdot x+0\cdot x^2+0\cdot x^3+0\cdot x^4\\ x& \to p_2(x)=1+x+x^2=1+1\cdot x+1\cdot x^2+0\cdot x^3+0\cdot x^4\\ x^2& \to p_3(x)=1+x+x^4=1+1\cdot x+0\cdot x^2+0\cdot x^3+1\cdot x^4\end{array}$$ $$\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\text{ or? }\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 0& 1& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right]$$ $$\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}2\\ 0\\ 0\end{array}\right]=\left[\begin{array}{c}2\\ 2\\ 0\\ 0\end{array}\right]$$ $$\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}2\\ 5\\ -3\end{array}\right]=\left[\begin{array}{c}4\\ 4\\ 5\\ -3\end{array}\right]$$

Lecture 21

• Write somewhere
• Let $(a,b,c)\in {\mathbb{R}}^3$ with the standard basis. Then we can express $(a,b,c)=a{e}_1+b{e}_2+c{e}_3$ we can express this in terms of coordinate vectors such that $[(a,b,c){]}_{SB}=(a,b,c)$
• Here is a better example : Let $B=\{1,x,..,x^n\}\subseteq F[x{]}_{\le n}$ be the basis, hence we can express polynomials $[a_1+a_{2}x+...,+a_n{x}^n{]}_B=(a_1,a_2,...,a_{n+1})\in F^{n+1}$ which gives us bijections between vector spaces!

Lemma : Coordinate Vectors in Linear Transformations

If $[u{]}_B=(a_1,...,a_n),u\in V,a_i\in F$, then

$$[T(u){]}_C=\left[\begin{array}{c}{\sum }_{j=1}^n{a}_{1j}{a}_j\\ {\sum }_{j=1}^n{a}_{2j}{a}_j\\ ⋮\\ {\sum }_{j=1}^n{a}_{mj}{a}_j\\ \end{array}\right]$$

Proof

$$\begin{array}{r}T(u)=T(\sum _{j=1}^n{a}_j{u}_j)=\sum _{j=1}^n{a}_{j}T(u_j)=\sum _{j=1}^n{a}_j\sum _{i=1}^m{a}_{ij}{w}_i=\sum _{i=1}^m\sum _{j=1}^n{a}_{ij}{a}_j{w}_i\in W\end{array}$$

Remark : This is basically multiplying a matrix with a Vector! $A=(a_{ij}),m\times n$, a vector $a=(a_{i1}),n\times 1$, then we produce a $m\times 1$ vector $A\cdot a$, where the ith component is ${\sum }_{j=1}^n{a}_{ij}{a}_j$

Lets examine a matrix

The Motivation? MATRIX MULTIPICATION

Theorem : Matrix Multiplication

Let $V,W$ be vector spaces with bases $B=\{v_1,...,v_n\}\subseteq V,C=\{w_1,...,w_n\}\subseteq W$, and a $T:V\to W$ be a linear map, then

$$[T(u){]}_C=[T{]}_C^B\cdot [u{]}_B$$

If we define $[T{]}_C^B=(t_{ij})$, then $T(u_j)={\sum }_{i=1}^m{t}_{ij}{w}_i$

Digression : The Algebra of Linear Transformations

Groups, Rings, Fields, VectorSpaces

(Prop) Fun $(X,W)$ is a F.V.S. (The Soul Stone of Linear Algebra!)

Consider a set $X$ and a F.V.S. $W$, then all possible functions from $X\to W$ (denoted $Fun(X,W)$ or in set theory $W^X$) is a F.V.S

Proof $f,g\in Fun(X,W)$ and an arbitrary element $x\in X$ then we have to show that it is an abelian group under addition that respects scalar multiplication!

1. Abelian Group under Addition $(f+g)(x)=f(x)+g(x)=g(x)+f(x)(g+f)(x)\in W$

$\text{Since },f(x),g(x)\in W\text{Then it follows the axioms}$

2. Respects scalar multiplication $(a\cdot f)(x)=a\cdot f(x)$

Since $a\in F$ is an arbitrary scalar, and $f(x)\in W$, then $a\cdot f(x)\in W$ Therefore, it follows all of the vector space axioms, hence $Fun(X,W)$ is a vector space!

Why isn't $Fun(W,X)$ an F.V.S.

Why is this the so powerful

Think about endgame, the soul stone is able to take any soul and put it into any other soul, in this case, we can take the soul of the set and transform it into an FVS(Given that its being mapped into an FVS)! This powerful took is the backbone to why matrices work!

Homomorphisms and using the Soul Stone

• While the soul stone is quite unstable, we can make it more stable through homomorphism!

Homomorphism :

Homomorphism is a function in mathematics that preserves the structure between two algebraic structures. In our case, if we want to go between two FVS, say V and W, we want to define a vector space homomorphism over the same field $F$ to preserve the vector space properties!

Supose $X$ was an FVS, we will call it V, what do we get out of it?

1. From the prop, we can easily examine that $Fun(V,W)$ is a vector space
2. These mappings are also Vector Space Homomorphisms over the same field F

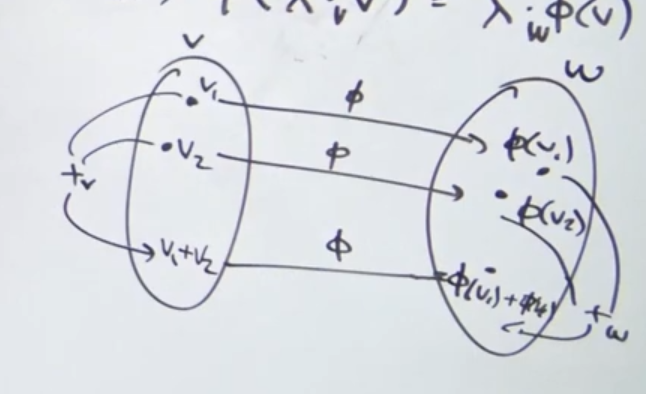
(prop) Linearity is a Vector Space Homomorphism

For any vector spaces $(V,{+}_V,{\cdot }_V),(W,{+}_W,{\cdot }_W)$ over the same field $F$, a function $\phi$ such that $\phi :V\to W$, $\phi$ is a vector homomorphism( samething as saying that $\phi$ is linear) if for any $v_1,v_2\in V,a,b\in F$ :

1. $\phi (v_1\text{SR}V+v_2)=\phi (v_1)\text{SR}W+\phi (v_2)$

2. $\phi (a\text{SR}V\cdot v)=a\text{SR}W\cdot \phi (v)$ $⟺$ $\phi (a\text{SR}V\cdot v_1\text{SR}V+b\text{SR}V\cdot v_2)=a\text{SR}W\cdot \phi (v_1)\text{SR}W+b\text{SR}W\cdot \phi (v_2)$

Visual :

Side note on linearity/linear maps

• Linear Algebra is an old subject, with its strongest roots dating back to the 19th century. Therefore a lot of Jargon has stuck with it until the 21st century. Using the concept of linearity(19th century Jargon) is the same ideas as a Vector Space Homomorphism over the same field(Contemporary Jargon), however notice how cacophonous this is, so linear is just nice to use
• Note : This specific construction preserves the vector space structure, meaning that it satisfies all 10 axioms of a vector space!
• For the rest of the notes, I will also omit the sub and super scripts if we know before hand that its a the Homomorphism satisfies linearity (Also known as a Linear Transformation)
• We will transition to $T$ and $S$ to denote Linear Transformations between two vector spaces -Visual : > [!note] Linear maps:

Proof $S:V\to W$ and $T:V\to W$. Then for any two vectors $v_1,v_2\in V$

1. $\begin{array}{rl}(S+T)(v_1+v_2)& =S(v_1+v_2)+T(v_1+v_2)\\ & =S(v_1)+S(v_2)+T(v_1)+T(v_2)\\ & =S(v_1)+T(v_1)+S(v_2)+T(v_2)\\ & =(S+T)(v_1)+(S+T)(v_2)\end{array}$
2. $\begin{array}{rl}(S+T)(a\cdot v)& =S(a\cdot v)+T(a\cdot V)\\ & =S(v_1)+S(v_2)+T(v_1)+T(v_2)\\ & =S(v_1)+T(v_1)+S(v_2)+T(v_2)\\ & =(S+T)(v_1)+(S+T)(v_2)\end{array}$

The space of all linear maps

• Credit :
• https://www.youtube.com/watch?v=asLWWwiWmMU

(prop) $HO{M}_F(V,W)$ is a Vector Space

Lets consider the subset $Fun(V,W)$ such that the functions are linear. $Ho{m}_F(V,W)=L(V,W)=\{T:V\to W\mid T\text{ is linear }\}$ then $Ho{m}_F(V,W)$ is a FVS

Proof (Simple) :D $Ho{m}_F(V,W)$ is a vectorspace, we must show it's a subspace. and we can show this through linearity!

1. Linearity proves closure under addition

Let define addition, for any vector $v\in V$ $\begin{array}{rl}+:Ho{m}_F(V,W)\times Ho{m}_F(V,W)& \to Ho{m}_F(V,W)\\ (T,S)& \mapsto T(v)+S(v)\end{array}$ We will also denote this short-hand $(T+S)(v)=T(v)+S(v)$ (T + S) is linear

Suppose we pick two vectors $v_1,v_2\in V$ and $a\in F$, then

1. $\begin{array}{rl}(T+S)(v_1+v_2)& =T(v_1+v_2)+S(v_1+v_2)\\ & =T(v_1)+T(v_2)+S(v_1)+S(v_2)\\ & =T(v_1)+S(v_1)+T(v_2)+S(v_2)\\ & =(T+S)(v_1)+(T+S)(v_2)\end{array}$
2. $\begin{array}{rl}(T+S)(a\cdot v)& =T(a\cdot v)+S(a\cdot v)\\ & =a\cdot T(v)+a\cdot S(v)\\ & =a\cdot (T(v)+S(v))\\ & =a\cdot ((T+S)(v))\end{array}$

1. Linearity proves closure under addition Let define addition, for any vector $v\in V$ $\begin{array}{rl}\odot :F\times Hom(V,W)& \to Hom(V,W)\\ (a,T)& \mapsto (a\odot T)(v)\end{array}$ We also represent this operation as $(a\odot T)(v)=a\cdot T(v)$ $(a\odot T)(v)$ is linear

Suppose we pick vectors $v_1,v_2\in V$ and scalars $a,b\in F$

1. $\begin{array}{rl}(a\odot T)(v_1+v_2)& =a\cdot T(v_1+v_2)\\ & =a\cdot (T(v_1)+T(v_2)\\ & =a\cdot T(v_1)+a\cdot T(v_2)\\ & =(a\odot T)(v_1)+(a\odot T)(v_2)\end{array}$
2. $\begin{array}{rl}(a\odot T)(b\cdot v)& =a\cdot T(b\cdot v)\\ & =a\cdot b\cdot T(v)\\ & =b\cdot (a\cdot (T(v))\\ & =b\cdot ((a\odot T)(v))\end{array}$

Notation $L(V,W)=Ho{m}_F(V,W)\subseteq Fun(V,W)$, as it provides more detail, $L(V,W)$ is 19th century notation

I will denote

Function Compositions over Vector Spaces

Consider 3 vector spaces, $U,V,W$ and 2 functions $f:U\to V$ and $g:V\to W$. We can apply the same Composition rules to vector spaces as it can be composed as $g\circ f(u)=g(f(u))$

This naturally gives us the following map

$$\begin{array}{rl}Fun(V,W)\times Fun(U,V)& \to Fun(U,W)\\ (g,f)& \mapsto g\circ f\end{array}$$

Which can be restricted even further to : $Ho{m}_F(V,W)\times Ho{m}_F(U,V)\to Ho{m}_F(U,W)$

[!note] Linearity and Bilinearity

Compositions of Linear Maps are linear!

Proof $f\in Ho{m}_F(U,V),g\in Ho{m}_F(V,W),a_1,a_2\in F,u_1,u_2\in U$, then $(g\circ f(a_1{u}_1+a_2{u}_2))=g(f(a_1{u}_1+a_2{u}_2))=g(f(a_1{u}_1))+g(f(a_2{u}_2))=a_{1}g\circ f(u_1)+a_{2}g\circ f(u_2)$ j This guarantees us the fact that $Ho{m}_F(V,W)\times Ho{m}_F(U,V)\to Ho{m}_F(U,W)$ [!warning] This implies Bi-linearity! Def : Bilinearity : Linear with respect to each of the two arguments Claim : $Ho{m}_F(V,W)\times Ho{m}_F(U,V)\to Ho{m}_F(U,W)$ is Bi-linear [!check]- Proof

$$\begin{array}{rl}((b_1{g}_1+b_2{g}_2)\circ (a_1{f}_1+a_2{f}_2))(u)& =(b_1{g}_1+b_2{g}_2)((a_1{f}_1+a_2{f}_2)(u))\\ & =b_1(g_1((a_1{f}_1+a_2{f}_2)(u)))+b_2(g_2((a_1{f}_2+a_2{f}_2)(u)))\\ & =b_1(g_1(a_1{f}_1(u))+g_1(a_2{f}_2(u))))+b_2(g_2(a_1{f}_1(u))+g_2(a_1{f}_2(u))))\\ & =a_1{b}_1{g}_1(f_1(u))+a_2{b}_1{g}_1(f_2(u))+a_1{b}_2{g}_2(f_1(u))+a_2{b}_2{g}_2(f_2(u))\\ & =(a_1{b}_1{g}_1\circ f_1+a_2{b}_1{g}_1\circ f_2+a_1{b}_2{g}_2\circ f_1+a_2{b}_2{g}_2\circ f_2)(u)\end{array}$$

Remark : This bilinearity of rings $R$ be a ring with two binary operations, then the distribution laws mean that multiplication is bilinear

$$(a+b)\cdot (c+d)=a(c+d)+b(c+d)=ac+ad+bc+bd$$

There is some connection between the two!

Week 9

Lecture 22

1. Definition of Bilineatiy
2. Proved the Bilinearity
3. Showed Bilinearity in rings

Associativity of composition

Let $A,B,C,D$ be sets, and lets define the following functions $f:A\to B,g:B\to C,h:C\to D$, then : $h\circ (g\circ f)=(h\circ g)\circ f$

Proof $(h\circ (g\circ f))(x)=h((g\circ f)(x))=h(g(f(x))$ $((h\circ g)\circ f)(x)=(h\circ g)(f(x))=h(g(f(x))$

Remark $g\circ f$, $f\circ g$ might not make sense. Take $f:\mathbb{N}\to \mathbb{Z}x\mapsto x,g:\mathbb{Z}\to \mathbb{R},x\mapsto x^{-1}$ $g\circ f(20)=\frac{1}{20}$ $f\circ g(20)=f(\frac{1}{20})$ but note that $\frac{1}{20}\notin \mathbb{Z}$

Arbitrary composition of functions do not allow it to form a ring since given any

The Algebra of Endomorphisms!

We denote the set of Endomorphisms $End(V)=Ho{m}_F(V,V)$, so

$$End(V)=\{\text{all }T:V\to V|T\text{ is a linear map}\}$$

$End(V)$ forms a Ring under $+$ and $\cdot$

We can define addition and multiplication in the following ways: $+:End(V)\times End(V)\to End(V)$ $\circ :End(V)\times End(V)\to End(V)$ We can define two special elements as well (I will note that the zero function is often denoted by the zero element in the ring, but I want to introduce this new notation for even more clarity. It follows a similar style to the Identity) $Ze:V\to V,Ze(v)=\underline{0},\forall v\in V$ $Id:V\to V,Id(v)=v,\forall v\in V$ Collecting all of these items, we can form $End(V)$ into a ring! In particular, we can see that the $\circ$ distributes over $+$. Take note that $End(V)$ is not abelian as $f\circ g\ne g\circ f$ for some particular $f$ and $g$

Exercise Orthogonal Reflections

Lets examine $V={\mathbb{R}}^2$. One example of $End(V)$ would be the orthogonal reflections on the cartesian plane. For example, consider a line $l$ on the plane. We can consider the following transformation.

Hence using geometry, we can define one of the basis vectors as a rotation of $2\alpha$ around the origin, hence:

$$[S_{\ell }(e_1){]}_{SB}=\left[\begin{array}{c}\cos (2\alpha )\\ \sin (2\alpha )\end{array}\right]$$

Hence using geometry, we can define one of the basis vectors as a rotation of $2\alpha$ around the origin, hence:

$$[S_{\ell }(e_2){]}_{SB}=\left[\begin{array}{c}\cos (2\alpha -\frac{\pi }{2})\\ \sin (2\alpha -\frac{\pi }{2})\end{array}\right]=\left[\begin{array}{c}\sin (2\alpha ))\\ -\cos (2\alpha )\end{array}\right]$$

Giving us the following matrix for orthogonal reflections over any line

$$[S_{\ell }{]}_{SB}^{SB}=\left[\begin{array}{cc}\cos (2\alpha )& \sin (2\alpha )\\ \sin (2\alpha )& -\cos (2\alpha )\end{array}\right]$$

Method 2 : Curtesy of Stack exchange (Requires Matrix multiplication which will be proven later) Lets denote the Reflection over the any line $\ell$ that is angle $\theta$ away from the x-axis to be $F_{\theta }$. If we consider reflections over the x-axis ($F_0$) we get the following matrix

$$F_0=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$$

Now instead of considering rotations on a vector basis, suppose we rotate the line instead. Lets consider rotations by $\alpha$ around the orgin. First we rotate our line and vector back towards the origin, then reflect along the x-axis, then rotate it back to our original angle!

$$\begin{array}{rl}{F}_{\theta }& =R_{\alpha }{F}_0{R}_{-\alpha }\\ & =\left[\begin{array}{cc}\cos (\alpha )& -\sin (\alpha )\\ \sin (\alpha )& \cos (\alpha )\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\left[\begin{array}{cc}\cos (-\alpha )& -\sin (-\alpha )\\ \sin (-\alpha )& \cos (-\alpha )\end{array}\right]\\ & =\left[\begin{array}{cc}\cos (\alpha )& -\sin (\alpha )\\ \sin (\alpha )& \cos (\alpha )\end{array}\right]\left[\begin{array}{cc}\cos (-\alpha )& -\sin (-\alpha )\\ -\sin (-\alpha )& \cos (-\alpha )\end{array}\right]\\ & =\left[\begin{array}{cc}\cos (\alpha )& -\sin (\alpha )\\ \sin (\alpha )& \cos (\alpha )\end{array}\right]\left[\begin{array}{cc}\cos (\alpha )& \sin (\alpha )\\ \sin (\alpha )& -\cos (-\alpha )\end{array}\right]\\ & =\left[\begin{array}{cc}{\cos }^2(\alpha )-{\sin }^2(\alpha )& \cos (\alpha )\sin (\alpha )+\sin (\alpha )\cos (\alpha )\\ \sin (\alpha )\cos (\alpha )+\cos (\alpha )\sin (\alpha )& {\sin }^2(\alpha )-{\cos }^2(\alpha )\end{array}\right]\\ & =\left[\begin{array}{cc}\cos (2\alpha )& \sin (2\alpha )\\ \sin (2\alpha )& -\cos (2\alpha )\end{array}\right]\end{array}$$

Exercise : Composition of Reflections

Now Suppose we have two lines ${\ell }_1,{\ell }_2$ and consider that the angle from ${\ell }_1$ to ${\ell }_2$ is $\alpha$, then consider two vectors on each line, $v_1$ $v_2$ that lie on ${\ell }_1$ and ${\ell }_2$ respectively. Then

$S_{{\ell }_2}\circ S_{{\ell }_1}=R_{2\alpha }$ $S_{{\ell }_1}\circ S_{{\ell }_2}=R_{-2\alpha }$ (by the same construction)

---

$\ell$ (2, 5, -3) = 2 + 5x -3x^2 = 2(1+x) + 5(1+x+x^2) -3(1+x+x^4) = 4 + 4x + 5x^2 -3x

sin((1, 0))

→ sin(-x) = -sin(x) → cos(-x) = cos(x) →cos(x - pi/2) = -sin(x)*sin(-pi/2) = sin(x) sin(x - pi/2) = cos(x)sin(-pi/2) = -cos(2x) →sin(x+pi/2) = cos(x) → cos(x + pi/2) = -sin(x) cos(-2\alpha + pi/2) = -sin(-2\alpha) = sin(2\alpha) sin(-2\alpha + pi/2) = cos(-2\alpha) = cos(2\alpha) goal = (sin(2x), -cos(2x))

its a clockwise rotation around (-pi/2 + 2\alpha)

pi/2 - alpha

is alpha is 30

then beta is 60

so the rotation would end up in being in -30

-30 = -90 + 2 * 30

Lecture 23

Matrix Multiplication

Matrix Multiplication Operation $A=(a_{ij})$ be an $m\times n$ matrix and $B=(b_{jk})$ be an $n\times p$ matrix, then $A\cdot B=(c_{ik})$ where $c_{ik}={\sum }_{j=1}^n{a}_{ij}{b}_{jk}$

Let

Matrix Multiplication Representation in terms of Linear Transformations $U,V,W$ with bases $B=\{u_1,...,u_m\},C=\{v_1,...,v_n\},D=\{w_1,...,w_{\ell }\}$ respectively with 2 linear transpositions, $T:U\to V$ and $T^{\prime }:V\to W$, then $(T^{\prime }\circ T)=[T^{\prime }{]}_D^C\cdot [T{]}_C^B$

Suppose we have 3 vector spaces over a field F,

Proof

$$[T{]}_C^B=(t_{ij}),m\times n,[T^{\prime }{]}_D^C=(t_{jk}),n\times \ell$$ $$\begin{array}{rl}(T^{\prime }\circ T)(u_k)& =T^{\prime }(T(u_k))\\ & =T^{\prime }(\sum _{j=1}^m{t}_{jk}{v}_j)\\ & =\sum _{j=1}^m{T}^{\prime }(t_{jk}{v}_j)\\ & =\sum _{j=1}^m{t}_{kj}{T}^{\prime }(v_j)\\ & =\sum _{j=1}^m{t}_{ij}\sum _{i=1}^{\ell }{t}_{ij}^{\prime }{w}_i\\ & =\sum _{i=1}^{\ell }\left(\sum _{j=1}^m{t}_{ij}^{\prime }{t}_{jk}\right)\cdot w_i\end{array}$$

Rotations on ${\mathbb{R}}^2$ Lets define the following function (Or more sophistically linear transformation) on the coordinate plane(${\mathbb{R}}^2$) as the following. Take any point, (x, y). We can define a rotation around the origin by an angle $\theta$ in the following way, where $B$ is the standard Basis $[R_{\theta }{]}_B^B=\left[\begin{array}{cc}\cos (\theta )& -\sin (\theta )\\ \sin (\theta )& \cos (\theta )\end{array}\right]$ Here is an example of this working, take the point (1, 1) for example and we want to rotate it by $90°$ around the origin, we can think of it as just a standard "matrix multiplication"

R_{90 \degree}((1, 1)) = \begin{bmatrix} \cos(90 \degree) & -\sin(90 \degree)\\ \sin(90 \degree) & \cos(90 \degree) \end{bmatrix}\begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 & -1\\ 1 & 0 \end{bmatrix}\begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 0\cdot1 +0 \cdot-1 \\ -1\cdot1 + 0\cdot0 \end{bmatrix} = \begin{bmatrix} -1 \\ 1 \end{bmatrix}$$ Here is a visual of what we just did! ![[Pasted image 20240311114856.png|300]] # Big Proof Concept (Sum of Angles Formula!) - Rotation $a$ + Rotation $b$ = Rotation $a + b$, Hence you can conceptualize composition of these items as adding the rotation between the two angels. You apply rotation by angle $a$ 1st, then by angle $b$ second. This gives us that: $$R_{a} \circ R_{b} = R_{a + b} = R_{b + a}$$ This naturally gives us the following identity: $$[R_{a+b}]_B^B = [R_{a}]_B^B[R_b]_B^B$$ Giving us this beautiful result that $$[R_{a} \circ R_{b}]_B^B = [R_{a}]_B^B[R_b]_B^B$$ What does this tell us? It gives us a quick way to compute cos(a + b) and sin(a + b) as $$ \begin{aligned} \begin{bmatrix} \cos(a + b) & -\sin(a + b)\\ \sin(a + b) & \cos(a + b) \end{bmatrix} = \begin{bmatrix} \cos(a) & -\sin(a)\\ \sin(a) & \cos(a) \end{bmatrix} \begin{bmatrix} \cos(b) & -\sin(b)\\ \sin(b) & \cos(b) \end{bmatrix} \end{aligned} $$ Using the matrix multiplication techniques, we can easily see that $$ \begin{aligned} \cos(a + b) &= \cos(a)\cos(b) -\sin(a)\sin(b)\\ \sin(a + b) &= \sin(a)\cos(b) + \cos(a)\sin(b) \end{aligned} $$ # Extending this phenomenon Further $$\begin{aligned} \cos(2a) &= \cos(a)\cos(a) -\sin(a)\sin(a) = \cos^2(a) - \sin^2(a)\\ \sin(2a) &= \sin(a)\cos(a) - \cos(a)\sin(a) =2\sin(a)\cos(a) \end{aligned}$$ $$[R_{a + b + c}]_B^B = [R_a \circ R_b \circ R_c]_B^B = [R_{a}]_B^B[R_b]_B^B[R_{c}]_B^B$$

\begin{aligned} [R_a]_B^B[R_b]_B^B[R_c]_B^B &= \begin{bmatrix} \cos(a) & -\sin(a)\ \sin(a) & \cos(a) \end{bmatrix}\begin{bmatrix} \cos(a) & -\sin(a)\ \sin(a) & \cos(a) \end{bmatrix}\begin{bmatrix} \cos(a) & -\sin(a)\ \sin(a) & \cos(a) \end{bmatrix}\ &=\begin{bmatrix} \cos(a) & -\sin(a)\ \sin(a) & \cos(a) \end{bmatrix}\begin{bmatrix} \cos(a)\cos(b) -\sin(a)\sin(b) & -\sin(a)\cos(b) + \cos(a)\sin(b)\ \sin(a)\cos(b) - \cos(a)\sin(b) & \cos(a)\cos(b) -\sin(a)\sin(b) \end{bmatrix} \end{aligned}

Commutative Diagrams

Lecture 24

Change Of Coordinates Formula

Suppose V is a Vector Space over F and we are given two bases

$$\begin{array}{rl}B& =\{v_1,...,v_n\}\\ B^{\prime }& =\{v_1^{\prime },...,v_n^{\prime }\}\end{array}$$

Given any vector $v\in V$, there naturally exists two coordinate vectors

$$\begin{array}{rl}[v{]}_B& =(a_1,...,a_n)\in F^n\\ [v{]}_{B^{\prime }}& =(a_1^{\prime },...,a_n^{\prime })\in F^n\end{array}$$

These two coordinate vectors give natural rise to an identity transformation: $[Id{]}_{B^{\prime }}^B$ Combining our previous ideas,

$$\begin{array}{rl}[T{]}_{B^{\prime }}^B\cdot [v{]}_B& =[T(v){]}_{B^{\prime }}\\ [Id{]}_{B^{\prime }}^B\cdot [v{]}_B& =[v{]}_{B^{\prime }}\end{array}$$

(Remember that $Id(v)=v$!)

Commutative Diagram

Remark $[Id{]}_{B^{\prime }}^B$ you find the coordinate vectors $[v_j{]}_{B^{\prime }}$ that is a solution to : $x_1{v}_1^{\prime }+...+x_n{v}_n^{\prime }=v_j$

This is an easy computation as its all a system of linear equations. To find

Change of a Matrix of a linear map

Suppose $T:V\to W$ and $B\subseteq U,C\subseteq W$ be two bases. From the precious theorem, then $[T{]}_C^B=\left[\begin{array}{ccc}& & \\ ...& [T(v_j){]}_C& ...\\ & & \end{array}\right]$ Characterized by $[T(v){]}_C=[T{]}_C^B\cdot [v{]}_B$ Now choose another pair of bases, $B^{\prime }\subseteq V,C^{\prime }\subseteq W$, which will give rise to : $[T{]}_{C^{\prime }}^{B^{\prime }}=\left[\begin{array}{ccc}& & \\ ...& [T(v_j^{\prime }){]}_C& ...\\ & & \end{array}\right]$ $[T(v){]}_{C^{\prime }}=[T{]}_{C^{\prime }}^{B^{\prime }}\cdot [v{]}_{B^{\prime }}$

How are $[T{]}_C^B$ and $[T{]}_{C^{\prime }}^{B^{\prime }}$ related? $[[T{]}_{C^{\prime }}^{B^{\prime }}=[Id{]}_{C^{\prime }}^C\cdot [T{]}_C^B\cdot [Id{]}_B^{B^{\prime }}$

Commutative diagram $A\cdot [\alpha {]}_{B^{\prime }}=[T(v){]}_{C^{\prime }},\forall v\in V$. This is what we get in general!

$$\begin{array}{rl}[T(v){]}_{C^{\prime }}& =[Id{]}_{C^{\prime }}^C\cdot [T{]}_C^B\cdot \underset{[v{]}_B}{\underbrace{[Id{]}_B^{B^{\prime }}\cdot [v{]}_{B^{\prime }}}}\\ & =[Id{]}_{C^{\prime }}^C\cdot \underset{[T(v){]}_C}{\underbrace{[T{]}_C^B\cdot [v{]}_B}}\\ & =[Id{]}_{C^{\prime }}^C\cdot [T(v){]}_C\end{array}$$

Insert Second COmm diagram

Change of basis Matrix

Let V be a vector space. If this set $\{v_1^{\prime },...,v_n^{\prime }\}$ exists such that $a_j^{\prime }={\sum }_{i=1}^n{p}_{ij}{v}_i$ makes it a basis, then the matrix $P=(p_{ij})$ is called the change of basis matrix This is equivalent to saying to saying if $B^{\prime }=\{v_1^{\prime },...,v_n^{\prime }\}$ is a basis, then $P=[Id{]}_B^{B^{\prime }}$ Therefore, in order to changes bases, we need an n-tuple of vectors, meaning we need an $n\times n$ matrix

$P\ne [Id{]}_{B^{\prime }}^B$ Recall that $[v{]}_{B^{\prime }}=[Id{]}_{B^{\prime }}^B\cdot [v{]}_B$ Fact: $[Id{]}_B^{B^{\prime }}\cdot [Id{]}_{B^{\prime }}^B=[Id{]}_B^B=\left[\begin{array}{ccc}1& & 0\\ & \ddots & \\ 0& & 1\end{array}\right]$

How do we find $P$

Suppose we are given an old basis $B=\{v_1,...,v_n\}$ and a new basis $B^{\prime }=\{v_1^{\prime },...,v_n^{\prime }\}$ such that $v_j^{\prime }={\sum }_{i=1}^n{p}_{ij}{v}_i$, hence $P=[Id{]}_B^{B^{\prime }}$. Find either $[v{]}_{B^{\prime }}$ for some $[v{]}_B$ or $[v{]}_{B^{\prime }}$ for all $[v{]}_B$

Solution $v$ is fixed, then its coordinates $[v{]}_{B^{\prime }}$ are a solution to $x_1{v}_1^{\prime }+...+x_n{v}_n^{\prime }=v$ Which means that $P\cdot \left[\begin{array}{c}{x}_1\\ ⋮\\ x_n\end{array}\right]=[v{]}_B$ You can notice that we get the following solution! $P\cdot x=[v{]}_B⟺x=\underset{[Id{]}_{B^{\prime }}^B}{\underbrace{P^{-1}}}\cdot [v{]}_B$ Now suppose that $[v{]}_B$ is arbitrary, there are 2 equivalent answers, then $(a_1,...,a_n)$ with $a_j$ cant be specified. There are two ways to tackle this problem!

1. This is where you need $P^{-1}=[Id{]}_{B^{\prime }}^B$ Indeed, as $[(a_1,...,a_n){]}_{B^{\prime }}=P^{-1}\cdot \left[\begin{array}{c}{a}_1\\ ⋮\\ a_n\end{array}\right]$ In order to find $P^{-1}$, we just solve an n system $P\cdot X=\left[\begin{array}{ccc}1& & 0\\ & \ddots & \\ 0& & 1\end{array}\right]$ $P\cdot x^{(i)}=\left[\begin{array}{c}0\\ ⋮\\ 1\\ ⋮\\ 0\end{array}\right]$, where 1 is located in the jth component Hence, we just solve an $x\times 2n$ augmented matrix p_{11} & ... & p_{1n} &1 & & 0\\ & \ddots & & & \ddots & \\ p_{n1} & & p_{nn} & 0 & & 1 \end{array}\right]$$ Solving will give us : $$\left[\begin{array}{c c c|c c c} 1 & & 0 & & & \\ & \ddots & & & * & \\ 0 & & 1 & & & \end{array}\right]$$ Where the $*$ is $P^{-1} = [Id]^B_{B'}$

Week 10

God damn this theory is fucked and all over the place

• Prove that $Ho{m}_F(F,V)$ has a basis of n elements where half of them are left inverses of the dual of V and half of them are the right inverses of the dual V
• maybe show that it is a direct product?

Lecture 25 : The Dual Vector Space or Matrix Transposition

Matrix Transpose

Given $A=(a_{ij})\in M_{m,n}(F)$, we define its transpose $A^{\top }=(a_{ji})\in M_{n,m}(F)$

Example

\Cmatrix{}{1&2&3\\4&5&6}^\top = \Cmatrix{}{1&4\\2&5\\3&6}

What is the meaning of $A\mapsto A^{\top }$ ?

Linear Functionals and Dual Spaces

Let $V$ be a vector space over $F$, then its dual is defined to be

$$V^{\vee }=Ho{m}_F(V,F)$$

We call elements in $V^{\prime }$ linear functionals as a function $f:V\to F$ Note : Dual Spaces are also denoted as $V^{\ast }$ but i don’t like that notation. Also the start is often reserved for the adjoint!

$p\in \mathbb{R}[x]$, then a function from $T:\mathbb{R}[x]\to \mathbb{R}$ can be defined as $T(p)={\int }_0^{1}p(x)dx$

The space of integrable functions over a closed domain! take a polynomial

(Cor 1) $V^{\prime }$ forms a vector space

Proof $V$ is a vector space, and $F$ is a vector space, then $Ho{m}_F(V,F)$ forms a vector space!

Using Prop (Lecture 22), since

(Cor 2) Basis of $V^{\prime }$ (Dual Basis) Let $B=\{v_1,...,v_n\}\subset V$ be a basis of V, then we can define the dual basis as a list of ${\varphi }_1,...,{\varphi }_n\subset V^{\prime }$ to be functions such that ${\varphi }_j(v_k)=\{\begin{array}{ll}1& j=k\\ 0& o.w.\end{array}$ Then ${\varphi }_1,...,{\varphi }_n$ form a basis for $V^{\prime }$ Its all part of the Theory of Functions in Linear Algebra!

Standard basis of $Hom(F^n,F)$ Let $\{e_1,...,e_n\}$ be the standard basis of $F^n$, then ${\varphi }_j(e_k)=\{\begin{array}{ll}1& j=k\\ 0& o.w.\end{array}$ is the dual basis for the standard basis of $F^n$

Before looking at the proof, I recommend examining the next theorem to build intuition first!

Proof $v\in V$, then $\varphi (v)=\varphi ({\sum }_{j=1}^n{a}_j{v}_j)={\sum }_{j=1}^n{a}_j\varphi (v_j)$ $\varphi (v_j)={\sum }_{i=1}^n\varphi (v_j){\varphi }_i(v_j)$ Therefore, $\varphi (v)={\sum }_{j=1}^n{a}_j{\sum }_{i=1}^n\varphi (v_j){\varphi }_i(v_j)={\sum }_{i=1}^n\varphi (v_i)\stackrel{{\varphi }_i(v)}{\overbrace{\sum _{j=1}^n{a}_j\cdot {\varphi }_i(v_j)}}={\sum }_{i=1}^n\varphi (v_i){\varphi }_i(v)$ Hence ever linear functional is just $\varphi ={\sum }_{j=1}^n\varphi (v_j){\varphi }_j$

Pick a

(Cor 3) Every Linear Functional has a left! (The anti-Dual Space $V^{-\vee }$) Let $v_i^{\vee }\in V^{\vee }$ be a linear functional.

1. $v_i^{\vee }$ is injective:

Suppose $v_i^{\vee }(v)=0$, then $v_i^{\vee }({\sum }_{i=1}^n{a}_n{v}_n)={\sum }_{i=1}^n{a}_n{v}_i^{\vee }(v_n)=a_i{v}_i(v_i)$. Then $a_i{v}_i^{\vee }(v_i)=0⟺v_i^{\vee }(v_i)=0$ (since every element in a field has a multiplicative inverse)! By definition, we know that $v_i^{\vee }(v_i)=1\Rightarrow 0\cdot v_i^{\vee }(v_i)=\cdot 1⟺v_i^{\vee }(0\cdot v_i)=0⟺v_i^{\vee }(0\cdot v_i)=0$, meaning that the only element that maps to the additive inverse in $F$ is the 0 in $V$, therefore the kernal is trivial or $\ker v_i^{\vee }=\{0\}$

3. $v_i^{\vee }$ is surjective:

Pick an $a\in F$, $a=a\cdot 1=a\cdot v^{\vee }{v}_v=v_i^{\vee }(a\cdot v_i)$, therefore $Im{v}_i^{\vee }=F$

Therefore, every linear functional is invertible!. lets define its inverse as $v_i^{-\vee }$ where $v_i^{-\vee }\circ v_i^{\vee }\in F$ and $v_i^{\vee }\circ v_i^{-\vee }\in V$, given a dual space $V^{\vee }$ with a dual basis : $v_1^{\vee },...,v_n^{\vee }$, we have an ati-dual $V^{-\vee }=Ho{m}_F(F,V)$ with an anti-dual basis : $v^{-{\vee }_1},...,v^{-{\vee }_n}$,

(Cor 4) Basis of $Ho{m}_F(V,W)$ Suppose $B=\{v_1,...,v_n\}\subset V,C=\{w_1,...,w_m\}\subset W$ are bases. Using the props from before, we know that $Ho{m}_F(V,W)=Ho{m}_F(F,W)\times Ho{m}_F(V,F)$ Since both of these are vector spaces, we know the dimension will be $n+m$ by a bunch of theorems we did earlier(and later). hence we have basis of dimensions $n+m$ and basis will conprise of elements : $\{v_1^{\vee },...,v_n^{\vee },w_1^{-\vee },...,w_m^{-\vee }\}$

(Thm) Dimension of $V^{\prime }$

$Dim{V}^{\prime }=DimV$

Extended Proof $B=\{v_1,...,v_n\}\subset V$ and $T:V\to F$, then we can find an n-tuple $(a_1,...,a_n)\in F^n$ such that $T(v_i)=a_i,i\in [n]$. So this mapping looks like this

$$\begin{array}{rl}T:V^{\prime }& \to F^n\\ f& \mapsto (f(v_1),...,f_{(}{v}_n))\end{array}$$

1. $T$ is linear Let $f,g\in V^{\prime }$ and $a\in F$

1. $\begin{array}{rl}T(f)+T(g)& =(f(v_1),...,f(v_n))+((g(v_1),...,g(v_n))\\ & =(f(v_1)+g(v_1),...,f(v_n)+g(v_n))\\ & =((f+g)(v_1),...,(f+g)(v_n))\\ & =T(f+g)\end{array}$
2. $\begin{array}{rl}a\cdot T(f)& =a\cdot (f(v_1),...,f(v_n))\\ & =(a\cdot f(v_1),...,a\cdot f(v_n))\\ & =((a\cdot f)(v_1),...,(a\cdot f)(v_n))\\ & =T(a\cdot f)\end{array}$

2. $T$ is invertible $KerT=\{Ze\}\Rightarrow$ Injective. $Ze$ is the only function that maps $V\to F$ and is also the zero in the vector space of $V^{\prime }$ $ImT=F^n\Rightarrow$ Surjective : Let ${\varphi }_1,...,{\varphi }_n$ be the basis of $V^{\prime }$ and $a_1,...,a_n$ be the basis of $F^n$, then using lecture 20, we can define $T({\varphi }_j)=a_j$ and using the fact that $T$ is linear, then clearly the $ImT=F^n$

• Since T is invertible, $T^{-1}:F^n\to V^{\prime }$. We have proved that $T$ is an isomorphism!, hence $V^{\prime }\cong F^n$ meaning that $\dim V^{\prime }=\dim F^n$.
• This proof is fascinating as it illustrates what the linear transformation does under the hood. Let $a_j=(a_{j1},...,a_{jn})$ Then $f(v_j)=a_{jj}\Rightarrow T(f)=a_j$

Proof $\dim V^{\prime }=\dim Ho{m}_F(V,F)=\dim (V)\dim (F)=\dim (V)$ Note: We really haven't built enough machinery to prove the complex components of this, plus its really uninspiring

• Added Fact : Groups, Rings, Fields, VectorSpaces that : Every field is a V.S., but not all V.S. are fields!

THE BEUAUTY OF THE DUAL

Given any linear transformation $T:V\to W$ and their respective duals $V^{\vee },W^{\vee }$, the linear transformation is the composition pictured below!

(Lem) Matrices, Transpose, and Duals Oh My

Given a linear map, $T:V\to W$, it defines the map $\begin{array}{rl}{T}^{\top }:W^{\vee }& \to V^{\vee }\\ w^{\vee }& \mapsto T^{\top }\cdot w^{\vee }\end{array}$ such that $(F^{\top }\cdot f)(v)=f\circ F(v)=f(F(v))$

• Note : Composition of functions is a bi-linear operation : $(F,G)\mapsto F\circ G$ $⟺$ F is linear and G is linear, therefore, $F^{\top }$ is Linear

$\cdot$

What is matrix $T^{\top }$

Suppose we have fixed bases $B=\{v_1,...,v_n\}\subset V$ and $C=\{w_1,...,w_m\}\subset W$, hence $[F{]}_C^B\in M_{m,n}(F)$, then the dual bases, $B^{\top }=\{f_1,...,f_n\}\subset V^{\prime }$ and $C^{\top }=\{g_1,...,g_m\}\subset W^{\prime }$ Recall that $f_i(v_j)={\delta }_{ij},g_i(w_j)={\delta }_{ij}$ We obtain that $[F{]}_{B^{\top }}^{C^{\top }}\in M_{n,m}(F)$, hence these matrices are just transposes of each other!

(Lem) Linear maps and their transpose

If $[F{]}_C^B\in M_{m,n}(f)$, then $[F^{\top }{]}_{B^{\top }}^{C^{\top }}=(f_{ji})\in M_{n,m}(F)$

Proof $F^{\top }{g}_j={\sum }_{i=1}^n{f}_{ij}^{\top }{f}_i$ BY the definition of a dual basis: $f_{kj}^{\top }={\sum }_{i=1}^k{f}_{ij}^{\top }{f}_i(v_k)=F^{\top }{g}_j(v_k)=g_j(F(v_k))=g_j({\sum }_{\ell =1}^n{f}_{\ell k}(w_{\ell }))={\sum }_{\ell =1}^k{f}_{\ell k}{g}_j(w_{\ell })=f_{jk}$ Hence: $t_{jk}^{\top }=t_{kj}$

By definition

Lecture 26: Matrix Transpose Properties

(Prop) $(A^{\top }{B}^{\top })=(BA{)}^{\top }$

Why the swap? $U\stackrel{T}{\to }V\stackrel{S}{\to }W⟺S\circ T:V\to W$ Gives rise to $W^{\prime }\stackrel{S^{\top }}{\to }{V}^{\prime }\stackrel{T^{\top }}{\to }{U}^{\prime }⟺(S\circ T{)}^{\top }:W^{\prime }\to U^{\prime }$ They are the same map! so $T^{\top }\circ S^{\top }=(S\circ T{)}^{\top }$

Proof $(S\circ T{)}^{\top }f(v)=f(S\circ T(v))=f(S(T(v)))=S^{\top }f(T(v))=(T^{\top }(S^{\top }))(v)=(T^{\top }\circ S^{\top })f(v)$

The structure of a linear map

$T:V\to W,V\ne W$ (Rank-Nullity Theorem)

Goal : Given a linear map $T$, try to understand what it really does

19th century Interpretation

Given a linear map, $A:F^n\to F^m,v\mapsto A\cdot v$, Let $P,Q$ bet he change of bases matrices, w.r.t. A, then what is $Q^{-1}AP$

Question:

• Find matrices P, Q, such that $Q^{-1}AP$ is as nice as possible

(Thm) Change of Basis Matrix

Given finite dimensional vector spaces, $V,W$ and a transformation $T:V\to W$, then there exists bases, $B\subset V,C\subset W$ such that $[T{]}_C^B=\left[\begin{array}{cc}I& 0\\ 0& 0\end{array}\right]$, where $I\in M_{k,k}(F),[T{]}_C^B\in M_{\dim W,\dim V}(F)$

• Note : These bases are not unique, but any pair of such bases give the same matrix!

Week 12

• QUstion: Why does he reoder the matrix determinant differently. I am used to the notion of the matrix being $ad-bc$?
• FIX THIS HORENDOUS SHIT NOTATION WHEN ADDING MORE VECTOR SPACES
• “Mathematics is about thinking about theory, not so much about memorizing computation”
• “Some times mistakes happen, and saying sorry is okay. But sometimes its about how you fix the problem” - Pizza Guy
• Finish the proof for the direct sums

Lecture 31 : 4/1 : Bi-Linear Functionals!

Matrix? What is is? And what functions can be made using this?

Motivating example, Lets define the matrix: \Cmatrix{}{a_{11} & a_{12} \\ a_{21} & a_{22}} \in M_{2 \times 2}(F) Define $\det (A)=a_{11}{a}_{22}-a_{12}{a}_{21}\in F$ This definition is a function! $\det :M_{2\times 2}(F)$ Note: This function is a polynomial in 4 variables! $\det \in F[x_{11},x_{12},x_{21},x_{22}],\det =a_{11}{a}_{22}-a_{12}{a}_{21}$

Is this function Linear? $(x_{12},x_{21})$, then $x_{11},x_{22}$ can be considered linear. This is what is known as a bi-linear function!

NO: IT IS QUADRATIC, but it can be linear. Suppose we fix variables

End Goal : Construction of the determinant of the matrix! $F^n\times ...\times F^n\to F$

Trick: Realize that the deteminant, up to proportionality, is just n-linear anti-symmetric functions that maps

Bilinear Functions!

https://kconrad.math.uconn.edu/blurbs/linmultialg/bilinearform.pdf This who approach is just taking another idea we already discovered! Given Vector spaces $V,W$ with bases $B,C$, then the linear map $T:V\to W$ is the same as the set of n-tuples $\{w_1,...,w_n\}\subset W$ such that $T(v_j)=w_j,j\in [j],(T(v)={\sum }_{j=1}^{n}T(a_j{v}_j)={\sum }_{j=1}^n{a}_j{w}_j)$ Another example: $V^{\prime }$ has basis $\{{\phi }_1^V,...,{\phi }_1^V\}$ with dual $\{v_1,...,v_n\},{\phi }_i^V(v_j)={\delta }_{ij}$ WE COME BACK TO THE DELTA FUNCTIONS! $f={\sum }_{j=1}^n{b}_j{\phi }_j^V⟺f(v_j)=b_j⟺f({\sum }_{j=1}^n{a}_j{v}_j)={\sum }_{j=1}^n{a}_j{b}_j$

AN even further generalization

Bilinear Functionals

Let $V_1,V_2$ be vector spaces, and define a map $\begin{array}{rl}B:V_1\times V_2& \to F\\ (v_1,v_2)& \mapsto B(v_1,v_2)\end{array}$. We say $B$ is BiLinear if linear respective to each argument when another is fixed ie. $B(a_1{v}_{11}+a_2{v}_{12},v_2)=a_{1}B(v_{11},v_2)+a_{2}B(v_{12},v_2)$ $f(v_1,b_1{v}_{21}+b_2{v}_{22})=b_{1}B(v_1,v_{21})+b_{2}B(v_1,v_{22})$ $\forall a_i,b_i\in F,v_1\in V_1,v_2\in V_2$ If $B$ is BiLinear, then we can express it as one summation : $B(v_1,v_2)=B({\sum }_{i=1}^m{a}_i{v}_{1i},{\sum }_{j=1}^n{b}_i{v}_{2i})={\sum }_{i=1}^m{a}_{i}B(v_{1i},{\sum }_{j=1}^n{b}_i{v}_{2i})={\sum }_{i=1}^m{\sum }_{j=1}^n{a}_i{b}_{j}B(v_{1i},v_{2i})$ One take away is recall how distribution works, so the order of i and j can be different! 3

Distribution on Rings $R$ is a ring!, then the two distribution laws show that $\cdot :R\times R\to R$ is bilinear!$(a_1+a_2)(b_1+b_2)={\sum }_{i,j}{a}_i{b}_j$

If

A note on certain linear functionals: ${\sum }_{i=1}^n{\sum }_{j=1}^n{a}_i{b}_{j}B(v_{1i},v_{2i})={\sum }_{i,j\in [n]}{a}_i{b}_{j}B(v_{1i},v_{2i})$

The linear functionals we are going to examine in this next section will involve examining vectorspaces of the same dimension : n, so we will compress the notation even further below :

The set of all Bilinear Functionals $Ho{m}_F(V_1\times V_2,F)\subset Fun(V_1\times V_2,F)$ Other sources may use $Ho{m}_F(V_1\times V_2,F)=Ho{m}_F(V_1,V_2;F)=L(V_1,V_2;F)$

1. $Ho{m}_F(V_1\times V_2,F)$ is a FVS (Check lecture 18) Examine that $V_1\times V_2$ is a vectorspace, then done!

What is the basis of $Ho{m}_F(V_1\times V_2,F)$

We know the basis of $Ho{m}_F(V,F)$ to be ${\phi }_1^V,...,{\phi }_n^V$ Lets denote the bases and dual bases as followed, $iin[\dim V_1],j\in [\dim V_2]$: $B_1=\{v_{1i}\}\subset V_1$ $B_2=\{v_{2j}\}\subset V_2$ $B_1^{\vee }=\{v_{1i}^{\vee }\}\subset V_1^{\vee }$ $B_2^{\vee }=\{v_{2j}^{\vee }\}\subset V_2^{\vee }$ We can then determine a pair of bi-linear maps by the following: $B:V_1\times V_2\to F,B(v_1,v_2)\in F$ $\begin{array}{r}B(\sum _{i=1}^n{a}_{1i}{v}_{1i},\sum _{j=1}^n{a}_{1j}{v}_{2j})=\sum _{i,j}{a}_{1i}{b}_{2j}\stackrel{\in F}{\overbrace{B(v_{1i},v_{2j})}}\end{array}$ This function is quadratic!, namely : $B(v_{1i},v_{2j})={\sum }_{k,l}B(v_{1i},v_{2j})v_{1i}^{\vee }(v_{1k})v_{2j}^{\vee }(v_{2l})$ B(v_1, v_2) = \sum_{i, j} a_{1i}b_{2j} \sum_{k,l} B(v_{1i}, v_{2j})v^{\vee}_{1i}(v_{1k})v^{\vee}_{2j}(v_{2l})$$$$ = \sum_{i,j} B(v_{1i}, v_{2j})\overbrace{v^{\vee}_{1i}(v_{1k})}^{\delta_{ik}}\overbrace{v^{\vee}_{2j}(v_{2l})}^{\delta_{jl}} = B(v_{1k}, v_{2l}) 2) The monomial : ${\phi }_i^{V_1}\cdot {\phi }_j^{V_2}$ is bilinear

1. fix ${\phi }_{\cdot }^{V_1}$ then ${\phi }_{\cdot }^{V_2}$ is linear. Or fix ${\phi }_{\cdot }^{V_2}$, then ${\phi }_{\cdot }^{V_1}$ is linear
2. Therefore, $\{{\phi }_i^{V_1}\cdot {\phi }_j^{V_2},i,j\}$ spans $Ho{m}_F(V_1\times V_2,F)$

(Lem) $\{{\phi }_i^{V_1}\cdot {\phi }_j^{V_2},i,j\}$ are all linearly independent!

Proof ${\sum }_{ij}{a}_{ij}{\phi }_i^{V_1}{\phi }_j^{V_2}=0$, then ${\sum }_{ij}{a}_{ij}{\phi }_i^{V_1}{\phi }_j^{V_2}(v_{1k},v_{2l})={\sum }_{ij}{a}_{ij}{\phi }_i^{V_1}(v_{1k}){\phi }_j^{V_2}(v_{2l})=a_{kl}$, Therefore, all $a_{kl}=0\Rightarrow$ the L.D. relation is trivial!

Suppose

Therefore, the basis of $L(V_1,V_2;F)$ consists of elements of the form : $v_{1i}^{\vee }\cdot v_{2j}^{\vee }$ for all combinations of i and j

$Ho{m}_F(F^2,F^2;F)=span\{v_{11}^{\vee }\cdot v_{21}^{\vee },v_{11}^{\vee }\cdot v_{22}^{\vee },v_{12}^{\vee }\cdot v_{21}^{\vee },v_{12}^{\vee }\cdot v_{22}^{\vee }\}$ We know that $\det \in Ho{m}_F(F^2,F^2;F)$ hence we can define the usual $\det =a_{11}{a}_{22}-a_{12}{a}_{21}=v_{11}^{\vee }\cdot v_{22}^{\vee }-v_{12}^{\vee }\cdot v_{21}^{\vee }$

Consider the following Vector Space :

Cartesian Product of Vector Spaces

• Examples and Proof Provided by Axlers Book

Example ${\mathbb{R}}^2\times {\mathbb{R}}^3=\{((x_1,x_2),(x_3,x_4,x_5))\mid x_i\in \mathbb{R},i\in [5]\}$ ${\mathbb{R}}^5=\{(x_1,x_2,x_3,x_4,x_5)\mid x_i\in \mathbb{R},i\in [5]\}$ Note the following: ${\mathbb{R}}^2\times {\mathbb{R}}^3\ne {\mathbb{R}}^5$ $T((x_1,x_2),(x_3,x_4,x_5))=(x_1,x_2,x_3,x_4,x_5)\Rightarrow {\mathbb{R}}^2\times {\mathbb{R}}^3\cong {\mathbb{R}}^5$

Consider the following vector spaces

Given F.V.S.'s $V_1,...,V_n$, then ${\text{bigtimes}}_{i=1}^n{V}_i$ forms a F.V.S. Lets consider what this looks like as a set: ${\text{bigtimes}}_{i=1}^n{V}_i=\{(v_1,...,v_n)\mid v_i\in V_i,i\in [n]\}$ Lets define the following operations : $+:{\text{bigtimes}}_{i=1}^n{V}_i\times {\text{bigtimes}}_{i=1}^n{V}_i\to {\text{bigtimes}}_{i=1}^n{V}_i:$ $(v_1,...,v_n)+(w_1,...,w_n)=(v_1+w_1,...,v_n+w_n)$ $\cdot :F\times {\text{bigtimes}}_{i=1}^n{V}_i\to {\text{bigtimes}}_{i=1}^n{V}_i:$ $a\cdot (v_1,...,v_n)=(a\cdot v_1,...,a\cdot v_n)$

Proof $u,v,w\in {\text{bigtimes}}_{i=1}^n{V}_i$ and scalars $a,b\in F$

1. Closure under addition:

$u,v\in {\text{bigtimes}}_{i=1}^n{V}_i,u+v\in {\text{bigtimes}}_{i=1}^n{V}_i$

2. Associativity

$u,v\in {\text{bigtimes}}_{i=1}^n{V}_i$ $u+v=(u_1+v_1,...,u_n+v_n)=(v_1+u_1,...,v_n+u_n)=v+u\in {\text{bigtimes}}_{i=1}^n{V}_i$

3. Commutativity

$(u+v)+w=(u_1+v_1,...,u_n+v_n)+w=(u_1+v_1+w_1,...,u_n+v_n+w_1)$ $=(v_1+w_1+u_1,...,v_n+w_1+u_n)=(v_1+w_1,...,v_n+w_1)+u$ $=u+(v_1+w_1,...,v_n+w_1)=u+(v+w)$

4. Identity

$0=(0,...,0)$ $0+v=(0+v_1,...,0+v_n)=v=(v_1+0,...,v_n+0)=v+0$

5. Inverse

Pick any vector v, then $v+u=0\Rightarrow (v_1+u_1,...,v_n+u_n)=(0,...,0)\Rightarrow v_i+u_i=0⟺u_i=-v_i\Rightarrow u=(-v_1,...,-v_n)$

6. Scalar Multiplication Closure

$a\cdot v=(a\cdot v_1,...,a\cdot v_n)\in {\text{bigtimes}}_{i=1}^n{V}_i$

8. Distribution Properties

$a\cdot (u+v)=(a\cdot (u_1+v_1),...,a\cdot (u_n+v_n))$ $=(a\cdot u_1+a\cdot v_1,...,a\cdot u_n+a\cdot v_n)=a\cdot u+a\cdot v$ $(a+b)\cdot v=((a+b)\cdot v_1,...,(a+b)\cdot v_n)=(a\cdot v_1+b\cdot v,...,a\cdot v_n+b\cdot v_n)=a\cdot v+b\cdot v$

(prop) $\dim {\text{bigtimes}}_{i=1}^n{V}_i={\sum }_{i=1}^n\dim V_i$

Proof $B_i$ denote the basis of vectorspace $V_i$, where it contains $\dim V_i$ vectors. Lets also denote $0_{V_i}$ to be the additive identity of vector space $V_i$ Claim : the basis of $B$ of ${\text{bigtimes}}_{i=1}^n{V}_i$ can be split up based on the dimension of each vector space $V_i$ ex) cartesian product of 2 vector spaces: $B=\{v_1,...,v_{\dim V_1},v_{\dim V_1+1},...,v_{\dim V_1+\dim V_2}\}$

(Lem 1) : Given a F.V.S. V, its additive identity, $\{0_V\}$ forms a subspace

Proof

1. Closure under addition:

$0_V+0_V=0_V$

2. Scalar multiplication:

$a\cdot 0_v=0_v$

3. Additive Identity Exists:

Trivial by construction

Since its a subspace, and by prop…471-addbacklink, then $\{0\}$ is also a vectorspace!

(Lem 2) Given F.V.S. V, W, $\{0_W\}\times V$ and $V\times \{0_W\}$ are vector spaces with the same dimension as V

Proof $\begin{array}{rl}T:\{0_W\}\times V& \to V\\ (0_W,v)& \mapsto v\end{array}$ is an isomorphism

1. $KerT=\{(0,0)\}$

By construction of the homomorphism, that is the only element that maps to 0.

3. $ImT=V:$

$T(0,v)=T({\sum }_{i=1}^{\dim V}{a}_i\cdot 0,{\sum }_{i=1}^{\dim V}{a}_i{v}_i)$ $={\sum }_{i=1}^{\dim V}{a}_i\cdot T(0,v_i)={\sum }_{i=1}^{\dim V}{a}_i{v}_i$

The proof for the other direction is entirely the same,

Now, for every vector space $V_i$, construct vector spaces of the same size by using the following cartesian product : $\{0_{V_j}\}{\text{bigtimes}}_{j=1}^{i-1}{V}_i{\text{bigtimes}}_{k=i+1}^n\{0_{V_k}\}$ be a vector space called $W_i$. Claim: $V={⨁}_{i=1}^n{W}_i$

1. ${\sum }_{i=1}^n{W}_i\subset V$ Trivial
2. ${\bigcap }_{i=1}^n{W}_i=\{0\}$ Trivial Therefore, $V={⨁}_{i=1}^n{W}_i={\sum }_{i=1}^n\dim V_i$

Fact

In an additive category, such as abelian groups and vector spaces over a field F, the cartesian product and the direct-sum are the same thing! https://math.stackexchange.com/questions/39895/the-direct-sum-oplus-versus-the-cartesian-product-times https://en.wikipedia.org/wiki/Biproduct https://en.wikipedia.org/wiki/Additive_category Using this fact, we will use the direct sum to denote cartesian products, just because it looks cleaner: ${\text{bigtimes}}_{}$

Clearing up the confusion

• $Ho{m}_F(V\times W,F)=Ho{m}_F(V\oplus W,F)$ The latter is just better notation
• $Ho{m}_F(V\oplus W,F)\ne Ho{m}_F(V\otimes W,F)$ The former is all linear maps, the latter is all bi-linear maps!

Tensor Product

https://www.math3ma.com/blog/the-tensor-product-demystified

Notation and Definition dump

We say something is linear when $T(av+bw)=aT(a)+bT(b)$ We say something is bi-linear when $T(a{r}_1+b{r}_2,s)=aT(r_1,s)+bT(r_2,s)$ and $T(r,c{s}_1+d{s}_2)=cT(r,s_1)+dT(r,s_2)$ We say something is tri-linear when $T(a{r}_1+b{r}_2,s,t)=aT(r_1,s,t)+bT(r_2,s,t)$ $T(r,c{s}_1+d{s}_2,t)=cT(r,s_1,t)+dT(r,s_2,t)$ $T(r,s,e{t}_1+f{t}_2)=eT(r,s,t_1)+fT(r,s,t_2)$ We say something is ,multi-linear/Poly-Linear/N-Linear if $T(v_1,v_2,...a{v}_i+b{v}_i^{\prime },...v_n)=aT(v_1,v_2,...v_i,...v_n)+bT(v_1,v_2,...v_i^{\prime },...v_n)$

• Definition adapted from : https://www.math.lsu.edu/~lawson/Chapter9.pdf

BEST SLOGAN : “Tensor products of vector spaces are to Cartesian products of sets as direct sums of vectors spaces are to disjoint unions of sets.”\

Goated Sources:

1. https://www.math.brown.edu/reschwar/M153/tensor.pdf
2. https://people.math.harvard.edu/~elkies/M55a.10/tensor.pdf
3. https://www.cin.ufpe.br/~jrsl/Books/Linear%20Algebra%20Done%20Right%20-%20Sheldon%20Axler.pdf

BIG BOY TIME

$F^m\oplus F^n\cong F^{m+n}$ $F^m\otimes F^n\cong F^{mn}\cong {\mathcal{M}}_{m,n}(F)$ $Ho{m}_F(V_1,...,V_n,F)=Ho{m}_F({\otimes }_i{V}_i,F)$

Lecture 32: 4/5 :Multi-Linear Functionals

The connection between group theory and Linear Algebra!

In order to truly appreciate the beauty ok multi-linear functionals, we must explore Group theory, and it is the study of group theory which introduces the building blocks of symmetry! Review : 410 Branch

1. Group
2. Group Homomorphism
3. Symmetric Group
4. Sign Function : $sgn:S_k\to \{-1,1\}$

Fancy Bilinear Transfomation Definition

Recall $Ho{m}_F(F^2,F^2;F)=span\{x_{11}\cdot x_{21},x_{11}\cdot x_{22},x_{12}\cdot x_{21},x_{12}\cdot x_{22}\}$ Using group theory, we can more concisely write this span in the following way! $span\{x_{11}\cdot x_{21},x_{11}\cdot x_{22},x_{12}\cdot x_{21},x_{12}\cdot x_{22}\}=span\{x_{1\sigma (j)}{x}_{2\tau (j)},\forall \sigma ,\tau \in S_2,j\in [2]\}$

MultiLinear Functional

$Ho{m}_F(V_1,...,V_n,F)$ Which describe all n-linear functions from $V_1\times ...\times V_n\to F$, then Lets look at let $m_i=\dim V_i$ Hence the basis for $V_i$ will be denoted as $B_i=\{v_{i1},...,v_{i{m}_i}\}$ The dual basis : $B_i^{\vee }=\{v_{i1}^{\vee },...,v_{i{m}_i}^{\vee }\}=\{x_{i1},...,x_{i{m}_i}\}$

By definition, N linear functionals is the same thing as

The det operation is Anti-symmetric

Anti-symmetry: a relation is antisymmetric if $aRb=-bRa$ The determinant is anti-symmetric! $\det =a_{11}{a}_{22}-a_{12}{a}_{21}=-(a_{21}{a}_{12}-a_{22}{a}_{11})$ What we basically did was swap $(a_{11},a_{12})\leftrightarrow (a_{21},a_{22})$

Concrete Example : $L({\mathbb{R}}^2,{\mathbb{R}}^2;\mathbb{R})$

Week 13

Lecture 33: 4/8 : Decomposition of Bi-Linear Maps and Intro to K-Linear maps

(Lem) $L(V,;F))=L^{sym}(V,V;F)\oplus L^{asym}(V,V;F)$

Suppose we consider two linear maps $\Lambda ,{\Lambda }^{\prime }:L(V^{\times 2};F)\to L(V^{\times 2};F)$ such that (\Lambda B) (v_1, v_2) = \frac{1}{2}(B(v_1, v_2) + B(v_2, v_1))$$$$(\Lambda'B) (v_1, v_2) = \frac{1}{2}(B(v_1, v_2) - B(v_2, v_1)) These are known as Symmetrizers

(Lem) $\Lambda \in L^{sym}(V^{\times 2};F)$ and ${\Lambda }^{\prime }\in L^{asym}(V^{\times 2};F)$ $(\Lambda B)(v_1,v_2)=\frac{1}{2}(B(v_1,v_2)+B(v_2,v_1))=\frac{1}{2}(B(v_2,v_1)+B(v_1,v_2))=(\Lambda B)(v_2,v_1)$

$\Lambda \in L^{sym}(V^{\times 2};F)$ $({\Lambda }^{\prime }B)(v_1,v_2)=\frac{1}{2}(B(v_1,v_2)-B(v_2,v_1))=-\frac{1}{2}(B(v_2,v_1)-B(v_1,v_2))=-({\Lambda }^{\prime }B)(v_2,v_1)$ ${\Lambda }^{\prime }\in L^{asym}(V^{\times 2};F)$

Proof 1) $L^{sym}$ and $L^{asm}$ give a basis for $L$

1. $L=L^{sym}+L^{asym}$

Suppose that we pick a $B\in L(V^{\times 2};F)$. Observe that $B(v_1,v_2)=(\Lambda B)(v_1,v_2)+({\Lambda }^{\prime }B)(v_1,v_2)$ hence $L(V^{\times 2};F)=L^{sym}(V^{\times 2};F)+L^{asym}(V^{\times 2};F)$

2. $L^{sym}(V^{\times 2};F)\cap L^{asym}(V^{\times 2};F)=\{0\}$

Suppose $B\in L^{sym}(V^{\times 2};F)\cap L^{asym}(V^{\times 2};F)$, then $B(v_1,v_2)=-B(v_2,v_1)=-B(v_1,v_2)⟺2B(v_1,v_2)=0$ hence $L^{sym}(V^{\times 2};F)\cap L^{asym}(V^{\times 2};F)=\{0\}$

Therefore, $L(V^{\times 2};F)=L^{sym}(V^{\times 2};F)\oplus L^{asym}(V^{\times 2};F)$

Proof 2) Symmetrizers are projections $\Lambda$ is a projection of $L^{sym}(V^{\times 2};F)$ along L^{asym}(V^{\times2}; F)$$\Lambda' is a projection of $L^{asym}(V^{\times 2};F)$ along $L^{sym}(V^{\times 2};F)$ Find their Kernal and Images

Generalization : K-linear maps

Suppose we consider the following vector space :

• $V_1,...,V_k=V$, $\dim V_i=n,i\in [k]$

  • (Note, these are the same vector space, but with different bases)

• Bases : $B_i=\{v_{ij},j\in [n]\}\subset V_i$

• We will use this shorthand $L(V_1,...,V_k)=L(V^{\times k};F)$

Special Maps

Symmetric Maps $B\in L(V^k;F)$, $B$ is symmetric if: $B(v_1,...,v_k)=B(v_{\sigma (1)},...,v_{\sigma (k)}),\forall \sigma \in S_k$

Let

Anti-Symmetric Maps (or Skew-Symmetric) $B\in L(V^k;F)$, $B$ is Anti-Symmetric if: $B(v_1,...,v_k)=-B(v_k,...,v_1)$

Let

Alternating maps $B\in L(V^k;F)$, $B$ is Alternating if: $B(v,...,v)=0,\forall v$

Let

Lecture 34 : 4/10 Groups acting on Vector Spaces

More Defintions

General Linear Group Group Actions Symmetric Group Sign Function

Why do we need groups?

Because we can use groups to act on sets, which is helpful in counting the number of elements in a basis! A groups purpose in life is to act on things

Useful Properties :

1. $S_k$ acts on $F[x_1,...,x_k]$ ex) Let $\sigma =(132)$ and $f(x)=x_1^2{x}_2$ $\sigma f=x_3^2{x}_1$

Prove $S_k\cdot F[x_1,...,x_k]$ defines a group action

$F:F(b_1,...,b_n)=F(b_{i_1},...,b_{i_k})$

A try :

F is antisymmetric if

$F(b_1,...,b_n)=\pm F(b_{i_1},...,b_{i_k})$

• Problem! Too many permutations!

Another try!

$F(b_1,...,b_n)=-F(b_1,...,b_i,b_j+1,...,b_k)$ $b_i⟺fixed(ij)$

More problematic than appears

look :

$F(b_1,b_2,b_3)=-F(b_3,b_2,b_1)$ $=-F(b_2,b_1,b_3)=F(b_2,b_3,b_1)$ $-F(b_3,b_2,b_1)$ !! It works out!!!

“swap of changing letters can be done in different ways!”

Perform different out of a simple permutation

Perm = the parity of the number of the same is the same

Perm = different computations of a simple permutation

Consider a $B\in L(V^{\times k};F)$ such that $B(v_1,...,v_k)=a_1\cdot ...\cdot a_k$

Now suppose we consider acting on this using $S_k$

$\sigma \cdot B(v_1,...,v_k)=B(v_{\sigma (1)},...,v_{\sigma (k)})$

remember one important fact about the symmetric group, their inverses! $\sigma (i)=j⟺i={\sigma }^{-1}(j)$

In order for our equations to match up, we need to consider the following : $B(v_1,...,v_k)=x_1\cdot ...\cdot x_k(v_1,...,v_k)$ $\sigma \cdot B(v_1,...,v_k)=B(v_{\sigma (1)},...,v_{\sigma (k)})=x_1\cdot ...\cdot x_k(v_{\sigma (1)},...,v_{\sigma (k)})$

in order for the two to be equal, we must actually permute the vertices of the functionals $x_{\sigma (1)}\cdot ...\cdot x_{\sigma (k)}(v_{\sigma (1)},...,v_{\sigma (k)})$

$L^{asym}({⨁}_{i=1}^k{V}_i,F)$

$B_i=\{v_i\}\subset V$ $B_i^{\top }={\phi }_i^{V_i}$ $i_1<...<i_k$

$F:(v_{i_1},...,v_{i_k})\mapsto a_{i_1}\cdot a_{i_k}$

$F:a_{i_1}{x}_{1i_1}...a_{i_k}{x}_{k{i}_k}$

Now define the antisymmetric group (or alternating, however this terminology is outdated)

number of choices : n choose k

dim $\dim L^{asym}({⨁}_{i=1}^k{V}_i,F)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)$

---

Question :

Suppose we examine a finite field of 2 elements ${\mathbb{F}}_2$ and we form a vector space of dimension 2 : ${\mathbb{F}}_2^2$

Examine the following :

$Fun({\mathbb{F}}_2,{\mathbb{F}}_2)$ Basis: $f_0,f_1,f_i(j)=\{\begin{array}{ll}1,& i=j\\ 0& o.w.\end{array}$ $\dim Fun({\mathbb{F}}_2,{\mathbb{F}}_2)=2$

$Fun({\mathbb{F}}_2^2,{\mathbb{F}}_2)$ $g_1,g_2,g_i(a_j)=\{\begin{array}{ll}1,& i=j\\ 0& o.w.\end{array}$ $\dim Fun({\mathbb{F}}_2^2,{\mathbb{F}}_2)=2$

$Fun({\mathbb{F}}_2^2,{\mathbb{F}}_2)\Rightarrow \#Fun({\mathbb{F}}_2^2,{\mathbb{F}}_2)=\#F_2^{\#F_2^2}=2^4=16$

$L^{(}{\mathbb{F}}_2,{\mathbb{F}}_2)$

Lecture : 4/12

1. Fix : $(i_j,...,i_k)$
2. $\sigma \in S_k$
3. $(...,v_{\sigma (i)}),...\mapsto sgn(\sigma )$ = $a{x}_{\sigma (1)i_1}{x}_{\sigma (2)i_2}\cdot ...\cdot x_{\sigma (k)i_k}$

$F\in span\{\sum sgn(\sigma )x_{\sigma (1)i_1}\cdot ...\cdot x_{\sigma (k)i_k}\}$

$a_i=i_b,a\pm b\Rightarrow a=0$ $F(...,\beta ,...)=0$ because it is symmetric

$F\in span\{{\sum }_{\sigma \in S_k}{x}_{\sigma (1)i_1}\cdot ...\cdot x_{\sigma (k),i_k}\}$

$S_2\cong Z/2$

k=2

$x_{1i}{x}_{2j}+x_{1j}{x}_{2i}$

$\sigma =(12)$

Each

${\sum }_{\sigma \in S_k}sign(\sigma )\cdot ...\cdot x_{\sigma (k)i_k}$

${\sum }_{{\sigma }^{\prime }\in S_k}\sigma (x_{1}i,...,x_{k{i}_j})$

is symmetric!

proof :

$\tau {\sum }_{\sigma \in S_k}={\sum }_{\sigma \in S_k}$

$\tau ({\sum }_{\sigma \in S_k}\sigma x_{1i}\cdot ...\cdot x_{k{i}_k})$

Want :

$\tau {\sum }_{\sigma \in S_k}sgn(\sigma )\sigma ={\sum }_{\sigma \in S_k}sgn(\sigma )v\sigma =\sum sgn(\sigma )\tau$

NOTES : remember, the $\{-1,1\}$ is an abelian group as it is isomorphic to $Z/2$

Therefore, the span is L.I., therefore it forms a basis!

Question : What are the dimensions!

$\dim L^{asm}(V^{\times k};F)=\#(i_1,<i_2<...<i_k,1<i_j\le \dim V)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)$

$k=2$ $x_{1i}{x}_{2i},i_1=i_2=i$

Span = $\sum x_{i_1}{x}_{i_2}...x_{i_k}$ $i_1\le ...\le i_k$

$\#$ combinations of combinatorions with repitions of k for out of dim V = $\left(\genfrac{}{}{0ex}{}{\dim V+k-1}{k}\right)$

$\dim =\left(\genfrac{}{}{0ex}{}{n+k-1}{k}\right)$

Segway into the Determinant!

$\dim L^{as}(V,...,V;F)=\left(\genfrac{}{}{0ex}{}{\dim V}{\dim V}\right)=1$

Focus on $L^{as}(F^n,...,F^n;F),\dim =1$

Let $F\subset L^{as}(\stackrel{ntimes}{\overbrace{F^n,...,F^n}};F)$ is determined up to a particular scalar is determined by $(e_1,...,e_n)$

$\det \subset L^{as}(F^n,...,F^n;F)$ is that functional whose value $\det (e_1,...,e_n)=1$, where $e_j$ is the famous epsilon function

Conventions : $\det (a_1,a_2,...,a_j,...,a_n)=\det \left[\begin{array}{c}{a}_1\\ ...\\ a_n\end{array}\right]=\det (a_{ij}),1\le i,j\le n$

$\det (a_{ij})=(-1)a_{\sigma (1)}{a}_{\sigma (2)}$ look at the formulas on the right!

$v$ is a vector, $v^{\vee }$ is a functional $v_1$ denotes the 1st basis vector in v, $v_1^{\vee }$ denote the first linear functional of v, This is near as $v_1^{\vee }(v_1)=1$ or $v_1^{\vee }{v}_1$ which looks exactly like the dot product in a sinple way : $x^{\top }y$

Week 14

Lec 36: 4/15

Determinant Properties!

: $det\in L^{as}(F^n{)}^{xn},F$ $\det (e_1,...,e_n)=1$

$\det (a_1,...,a_n)=\det \left(\begin{array}{c}{a}_1\\ ...\\ a_n\end{array}\right)$

$\det ((a_{ij}))={\sum }_{\sigma \in S_n}sgn(\sigma )a_{\sigma (1)1}...a_{\sigma (n)n}$

Properties :

1. det(A) $\ne 0⟺$ Invertible
2. $\det (A)=\det (A^{\top })$ $\det (A^{\top })={\sum }_{\sigma \in S_n}sgn(\sigma )$

Cancellation Law of Group Theory!

• $i=\sigma (j),j=\sigma (i)$

Fact : $sign(\sigma )=sign({\sigma }^{-1})$

Let $\det (A^{\top })={\sum }_{\sigma \in S_n}sgn(\sigma )b_{\sigma (1)a}...b_{\sigma (n)n}={\sum }_{\sigma \in S_n}sgn(\sigma )a_{{\sigma }^{-1}(1)a}...a_{{\sigma }^{-1}(n)n}=\det (A)$

E.R.O. V.S. Det(A)

if two rows are the same, $\det (\alpha ,\alpha )=0$ in most fields except characteristic 2

Properties :

1. $\det (A)=\det (rows)=\det (columns)$
2. $\det (equalrows)=0$
3. $\det (A_{i\to j}(\alpha )(A))=\det (A)$
4. $\det (M_i(a)A)=a\det (A)$
5. Row swap : $\det (PA)=-\det (A)$
6. $\det (upperrighttraingle)={\prod }_{i=1}^n{a}_{ii}$
   1. Why : $a_{\sigma (1)1}{a}_{\sigma (2)2}$
   2. This expression is nonzero $⟺$ $\sigma (j)=j$

upper right triangle : $A=\left[\begin{array}{cc}a& \star \\ 0& a\end{array}\right]$

(4 2 1 1) ←> (3 1 1 1)

Determinants as expansions by minors of a row/a column

$\det =\det (x_{ij})=3$

Recall, its linear in respect to the column!

A linear function : $x_{i_0}i,...,x_{i_0}n$

or $x_{1j_0},...,x_{n{j}_0}$

question : What is the coeeficient?!

$\det =?\cdot x_{11}+?\cdot x_2+...+?\cdot x_{1n}$ what are there existion marks

Adjoint of a matrix :

$(Adj(A){)}_{ij}=(-1{)}^{i+j}{M}_{ji}$

$A=\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]$ $Adj(A)=\left[\begin{array}{cc}{a}_{22}& -a_{12}\\ -a_{21}& a_{11}\end{array}\right]$

$(Adj)$

4 equations $⟺A\cdot Adj(A)=\left[\begin{array}{cc}\det (A)& 0\\ 0& \det (A)\end{array}\right]=[1001]$

Property!

1. $A^{-1}$ exists $⟺$ $\det (A)\ne 0$
2. $\det (A)\ne 0\Rightarrow A^{-1}Adj(A)\cdot \frac{1}{\det (A)}$
3. If $\det (A)=0\Rightarrow$ A is a 0 divisor! $\Rightarrow A\cdot Adj(A)=0$ $\det (Adj(A))=\det (A{)}^n$

---

Consider $\mathbb{Z}/2$ or a field on 2 elements

number o functions : $\#Fun(\mathbb{Z}\times \mathbb{Z},\mathbb{Z})=2^{2+2}=16$ unique functions

Claim!

In all characteristics, $L^{alt}(V,V;F)\subset L^{asym}(V,V;F)$ In not characteristic 2, $L^{alt}(V,V;F)=L^{asym}(V,V;F)$ In Characteristic 2, $L^{sym}(V,V;F)=L^{asym}(V,V;F)$ In characteristic not 2, $B(V,V;F)=L^{sym}(V,V;F)\oplus L^{asym}(V,V;F)$

Question 1) What is the total number of linear functions from

1. $\dim \mathbb{Z}/2\times \mathbb{Z}/2=2$, hence the dimension of all linear functions from $\mathbb{Z}/2\times \mathbb{Z}/2\to \mathbb{Z}/2$ is 2
2. $\dim L^{sym}(\mathbb{Z}/2,\mathbb{Z}/2;\mathbb{Z}/2)=\left(\genfrac{}{}{0ex}{}{2+2-1}{2-1}\right)=\left(\genfrac{}{}{0ex}{}{3}{1}\right)=3$
3. $\dim L^{asym}(\mathbb{Z}/2,\mathbb{Z}/2;\mathbb{Z}/2)=\left(\genfrac{}{}{0ex}{}{\dim V}{k}\right)=\left(\genfrac{}{}{0ex}{}{2}{2}\right)=1$
4. Claim 1: Every Symmetric Matrix is Antisymmetric
5. $\dim L^{sym}(\mathbb{Z}/2,\mathbb{Z}/2;\mathbb{Z}/2)\oplus \dim L^{asym}(\mathbb{Z}/2,\mathbb{Z}/2;\mathbb{Z}/2)=2+2-2=2$

Number of symmetric : $L^{sym}=\left(\genfrac{}{}{0ex}{}{n+k-1}{k}\right)$ $L^{alt}=\left(\genfrac{}{}{0ex}{}{\dim V}{k}\right)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)=L^{asym}$ Only in characteristic not 2

Case 1 k = 1: $\left(\genfrac{}{}{0ex}{}{n}{1}\right)+\left(\genfrac{}{}{0ex}{}{n}{1}\right)=2\cdot n=\dim L({\prod }_{i=1}^{n}V,F)$

case 2 : k = 2: $\left(\genfrac{}{}{0ex}{}{n+1}{2}\right)+\left(\genfrac{}{}{0ex}{}{n}{2}\right)=\frac{n+1(n)+n(n-1)}{2}=n^2$

case 3 : k = 3?><<dfsssss;‘x $\left(\genfrac{}{}{0ex}{}{n+2}{3}\right)+\left(\genfrac{}{}{0ex}{}{n}{3}\right)=$

$\left(\genfrac{}{}{0ex}{}{n-1}{k-1}\right)+\left(\genfrac{}{}{0ex}{}{n}{k}\right)$

In characteristic 2 : $L^{sym}=\left(\genfrac{}{}{0ex}{}{n+k-1}{k-1}\right)=L^{asym}$ $L^{alt}=\left(\genfrac{}{}{0ex}{}{\dim V}{k}\right)$

---

for bilinear maps, consider the following :

functionals on their own are not bi-linear, so we have to multiply!

consider the following for a V.S. of dimension 3 $x_1,x_2,x_3,y_1,y_2,y_3$

$B(v,v)=x_1$ is not bilinear, however, $x_1{y}_1+x_1$ is not bilinear. $x_1$ just doesn’t make sense! So, the basis of $B$ consist of 9 elements, choosing 1 from the left and 1 from the right $\left(\genfrac{}{}{0ex}{}{3}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{3}{1}\right)$

Question : what linear combination of ${\sum }_{ij}{a}_i\cdot x_i\cdot y_i=0?$

Observation: Consider a vector v with elements $(a_1,a_2,a_3)$, where each element is non-zero. then $x_1\cdot y_2(a_1,a_2,a_3)=a\cdot b=b\cdot a=x_i\cdot y_j(a_1,a_2,a_3)$

But notice something : $x_1(a_1,a_2,a_3)=a$, so inorder to find its counterpart $x_i(a_1,a_2,a_3)=b$, we should also consider that $y_1(a_1,a_2,a_3)=b$ is also a problem as $y_j(a_1,a_2,a_3)=b$

Lemma 1) : $x_i\cdot y_j(a_1,a_2,a_3)=x_j\cdot y_i(a_1,a_2,a_3)$ Proof : $x_i\cdot y_j(a_1,a_2,a_3)=x_i(a_1,a_2,a_3)\cdot y_j(a_1,a_2,a_3)=x_i(\sum {i=1}^3{a}_i{\alpha }_i)\cdot y_j(\sum {i=1}^3{b}_j{\alpha }_j)=a_i\cdot b_j=b_j\cdot a_i=x_j(\sum {j=1}^3{b}_j{\alpha }_i)y_i(\sum {i=1}^3{a}_j{\alpha }_i)=x_j\cdot y_i(a_1,a_2,a_3)$ Therefore, we can construct this monomial such that $x_i\cdot y_j-x_j\cdot y_i$

Note: If $i=j$, then our linear combination is not linearly independent as $x_i{y}_i-x_i{y}_i=0=0\cdot (x_i{y}_i-x_i{y}_i)$, therefore $i\ne j$ will always be 0 Conclusion, we just permute both i and j!, we need cycle that must be length 2: Lets consider $S_3$ (as our vector space is 3 dimensional). and let $\sigma \in S_3$, if we consider all options, of $x_{\sigma (1)}{y}_{\sigma (2)}$, we get the following :

e : $x_1{y}_2$ (12) : $x_2{y}_1$ (23) : $x_1{y}_3$ (13) : $x_3{y}_2$ $(123)$ : $x_2{y}_3$ (132) : $x_3{y}_1$

From this example, there is only permutation in which granted use the $x_2{y}_1$ element : (funily enough, its the ) Lemma 2)

The big thing we must consider is that while the vectorspaces have the same dimension, they might have different bases and thus different functionals!

Hence, we have witnessed that $x_1\cdot y_2(a_1,a_2,a_3)-x_2\cdot y_1(a_1,a_2,a_3)=0$! Its just a permutation of the indices!

Now consider the following :

ITS JUST $S_n$ acting on a set of n numbers, in our case, its

$S_n$ acting on $\{1,2\}$

$\left(\genfrac{}{}{0ex}{}{3}{2}\right)=\frac{3!}{2!\cdot 1!}$

$\frac{3!}{1!}=3!$

https://math.stackexchange.com/questions/242812/s-n-acting-transitively-on-1-2-dots-n

$S_n$ acting on $\{1,2,3\}$ = $\frac{3!}{2!}=3$

---

$\frac{4}{4}=1$ $S_n$ acting on $\{1,2,3,4\}$ is $\frac{4!}{3!}=4$

$\left(\genfrac{}{}{0ex}{}{4}{3}\right)=4$ $S_n$ acting on $\{1,2,3\}$ is $\frac{4!}{2!}$

$S_n$ acting on $\{1,2\}$ should have $\frac{4!}{2!}$

---

Naive Combinatorics

• https://math.stackexchange.com/questions/3210062/whats-the-difference-between-the-following-nk-1-choose-k-nk-1-choosek
• https://math.stackexchange.com/questions/4716950/combinations-with-repetition-nr-1-choose-r-1-nr-1-choose-r?rq=1

Consider a vector space of dimension n over a field F. Let $L(V^{(k)};F)$ denote all k-linear maps from $V\times ...\times V\to F$. Prove the dimension of $L^{sym}L(V^{(k)};F)$ or all symmetric k-linear maps is $\left(\genfrac{}{}{0ex}{}{n+k-1}{k}\right)$

Known Facts : $L(V^{(k)};F)=L^{sym}(V^{(k)};F)\oplus L^{asym}(V^{(k)};F)$ $L^{asym}(V^{(k)};F)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)$

Lec 38: 4/18

The Jordan Normal Form of a Linear Map (Ch 6, 7)

Problem : Given a space V, $\dim V<\infty$

Goal : Classify Linear maps $T:V\to V$ $L(V,V),\dim =n^2,F^{n^2}$

Produce a small (Finite) list of maps such that any $T:V\to V$ is equivalent to exactly 1 on the list

ex) We’ve seen an example

$\forall T:V\to W$, $\exists B\subset V,C\subset W$ such that

$[T{]}_C^B=\left[\begin{array}{cc}I& 0\\ 0& 0\end{array}\right]$

Classification of $L(V,V)$ such that $\{0,\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right],\left[\begin{array}{cc}1& 0\\ 1& 0\end{array}\right]...\left[\begin{array}{cc}I& 0\end{array}\right]\}$

$V=F^n,W=F^m$

$\forall T,\exists P,Q$ such that $Q^{-1}TP=\left[\begin{array}{cc}I& 0\\ 0& 0\end{array}\right]$ must T $\exists P,Q$ such that $Q^{-1}TP=\left[\begin{array}{cc}I& 0\\ 0& 0\end{array}\right]$ Want $T$ to quit $Q^{-1}TP$, any P, Q must

Marketing the problem precise : $L(F^n,F^n)\cong M_{n,n}(F)=\{(a_{ij}{)}^n\}$

Problem: CLassify matrices $(n\times n)$ up to similarity, i.e. $T$ is equvalent to $S$ if $T=P^{-1}SP$

Ex) $T_a:\mathbb{R}\to \mathbb{R},\alpha \mapsto a\cdot \alpha$

If allowed, $B\subset \mathbb{R},C\subset R,T_a$ is equivalent to $T_1$, where $a\ne 0$

Is that true

$T_a(1)=a$ $B=\{a\},C=\{a\}$

$[T{]}_{\{a\}}^{\{1\}}=1$

In general :

$[T{]}_v^v=a$ $v\mapsto a\cdot v$ When $|a|<1$ $(T_a{)}^n=T_{a^n}\to 0$

$[T^n{]}_B^B=([T{]}_B^B{)}^n$ Now, if its a square matrix : $([T^b{]}_C^B)=([T{]}_C^B{)}^n$

recall : $[T{]}_C^B\cdot [T{]}_B^C=[T^2{]}_B^B$

Fundamental result actually uses a neutering of the Jordan Normal Form

Hard problem : Simplification

Given : $\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]:{\mathbb{R}}^2\to {\mathbb{R}}^2$ Q) What does it do? Idea : Find $P=\left[\begin{array}{cc}w& x\\ y& z\end{array}\right]$, $\exists P^{-}1$ such that $P^{-1}\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]P$ is “Good”

Amazing Idea : “Good” means diagonal $T:F^n\to F^n$ such that $T=\left[\begin{array}{cc}{c}_1& 0\\ 0& c_n\end{array}\right]$ with a bunch of c_i in between Degrees of freedom are decoupled

$T:e_j\to c_j\cdot e_j$

Q) Is every matrix diagonizable? I.E. does there exist P for any T such that$P^{-1}TP=\left[\begin{array}{cc}{c}_1& 0\\ 0& c_n\end{array}\right]$

Example : Basically symmetric matrix!

$\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]\mapsto \left[\begin{array}{cc}?& 0\\ 0& ?\end{array}\right]$

What does it mean? $T=\left[\begin{array}{cc}{c}_1& 0\\ 0& c_n\end{array}\right]⟺T(e_j)=c_j{e}_j$

Eigen-Vector

Given $T:V\to V$, $v\in V$ is called an eigen vector if of eigen value c if $T(v)=c\cdot v$ and $v\ne 0$

T is digitizable if $\exists$ a basis of eigen vectors

Q) Is there atelast 1 eigenvector?

• Yes Iff $\det \ne 0⟺(T-cId)=0$ has a non-zero Solution $⟺\det (T-cId)=0$

eigenvalue $\approx$ characteristic $\#$ eigenvector $\approx$ characteristic vector

Characteristic Polynomial

The characteristic polynomial of $T:V\to V$ is $\det (T-xId)\in F[x]$

WE WANT EIGEN VALUES, so from now on, $F$ is algebraically closed $F=\text{C}$

Let V be a vector space over a field F of dimension n. find the dimension of all k-linear maps $B:\underset{k}{\underbrace{V\times ...\times V}}\to F$ : $L(V^{\times k};F)$

$\dim L(V^{\times k};F)=n^k$

Suppose n = 5, k = 3

$\dim L^{sym}(V^{\times k};F)=\left(\genfrac{}{}{0ex}{}{5+3-1}{3}\right)=\left(\genfrac{}{}{0ex}{}{7}{3}\right)=35$ $\dim L^{asym}(V^{\times k};F)=\left(\genfrac{}{}{0ex}{}{5}{3}\right)=10$

$\dim L(V^{\times k};F)=\dim L^{sym}(V^{\times k};F)\oplus \dim L^{asym}(V^{\times k};F)$

BUT $5^3\ne 45=35+10$

Lec 39 : 4/24 : Jordan Normal Form of a Matrix

Recall : $T:V\to V$ over F

$3=\mid T-xId\mid ={\prod }_j(c_j-x{)}^{m_j},{\sum }_j{m}_j=n$

$V_{c_j}=\ker (T-c_{j}Id)\ne 0$

$T$ diagonalizable $⟺$ $\oplus V_{c_j}=V$

Experimental Material :

Not every linear map is diagonalizable :

1. T : \Cmatrix{}{c & 1 & 0 & ... \\ 0 & c & 1 & 0 ...\\ \vdots \\ 0 & ... & c & 1 \\ 0 & ... & 0& c}
2. $T:{\text{C}}^n\to {\text{C}}^n$
3. ${\xi }_T(x)=(c-x{)}^n$

Ways to solve :

1. $(T-cId{)}^n={\chi }_T(T)$ Note : $(T-cId{)}^n=Ze:{\text{C}}^n\to {\text{C}}^n$

\Cmatrix{}{c & 1 & 0 & ... \\ 0 & c & 1 & 0 ...\\ \vdots \\ 0 & ... & c & 1 \\ 0 & ... & 0& c} \iff there is a chain

$e_1\stackrel{T-cId}{\to }0$ but

$e_n\stackrel{T-cId}{\to }...\stackrel{T-cId}{\to }{e}_1\stackrel{T-cId}{\to }0$

Also :

$\ker (T-cId{)}^n={\text{C}}^n$

2. Doing a concrete example

\Cmatrix{}{2 & 1 & -1\\ 2 & 2 & -1\\ 2 & 2 & 0} : \C^3 \to C^3

${\chi }_T(x)=-(x-1)(x-2{)}^3$

$({\text{C}}^3{)}_1:{\alpha }_1,\dim =1$ $({\text{C}}^3{)}_2:{\alpha }_2,\dim =1$

From this, this means its not diagonalizable

${\alpha }_1\stackrel{T-Id}{\to }0$ ${\alpha }_2\stackrel{T-2Id}{\to }0$ ${\alpha }_3\stackrel{T-cId}{\to }{\alpha }_2$ ${\alpha }_3\to {\alpha }_2=(0,1,0)$ ${\alpha }_3\stackrel{T}{\to }{\alpha }_2+2ds=(0,1,2)$ eignevectors :

$T({\alpha }_1)=1\cdot {\alpha }_1$

[T]_{\{\alpha_1, \alpha_2, \alpha_3\}} = \Cmatrix{}{1 & 0 & 0\\ 0 & 2 & 1\\ 0 & 0 & 2}

$C^3=\ker (T-Id)\oplus \ker (I-2Id{)}^2$

Fact : \ker(I-2Id)^2 = \Cmatrix{}{0 & 1\\ 0 & 0}^2 = \Cmatrix{}{0 & 0\\ 0 & 0}

B: The result :

(Def) Root space

The kernel : $\ker (T-c_{j}Id{)}^{m_j}$ is called the root space. It is denoted as : $V(c_j)$ Note :

1. $V_{c_j}\subset V(c_j)$, if $V_{c_j}=V(c_j)$, then it means that it is diagonalizable!
2. $\dim V(c_j)\ge 1$, we can also see that $\dim V(c_j)=m_j$
3. $V(c_j)\subset V$ is a subspace!

(Lem) $V(c_j)$ is a T-Invariant, i.e.

$T:V(c_j)\to V(c_j)$

Proof $\alpha \in V(c_j),(T-c_{j}Id{)}^{m_j},\alpha >0$ $(T-c_{j}Id{)}^{m_j}T\alpha =T\underset{m_j}{\underbrace{(T-c_{j}Id)}}\alpha =0$

(Thm)

1. $V=\oplus V(c_j)$ $({\text{C}}^3)=({\text{C}}^3)(1)$ ${\text{C}}^3(2)⊋({\text{C}}^3{)}_2$
2. For the restriction of $T$ to $V(c_j)$, each j, there is a basis $B$ of $V(c_j)$ such that bunch of blocks in the matrix : add photo each block being of the form… (add more photos)
3. The collection of sizes of blocks up to order, is independent of the basis!

Question : Are the sizes of the blocks dependent on the dimension of the root space?

Jordan Cell !

\Cmatrix{}{c_j & 1 & 0 & ... \\ 0 & c_j & 1 & 0 ...\\ \vdots \\ 0 & ... & c_j & 1 \\ 0 & ... & 0& c_j}

Suppose T is upper triangular, where the diagonals are denoted by $b_1,..,b_n$, then determinant is ${\prod }_j=b_j$

Now suppose its in the jordan normal form

$m_j=\sum$ sizes of all cells with $c_j$ on the diaganols

Cases and examples :

$\dim V=2$

2 cases! \Cmatrix{}{0 & *\\ 0 & *}, \Cmatrix{}{c_1 & 1\\ 0 & c_1}